Di che cosa parliamo
- Come ordinare elementi con shell sort
- Come usare il deep learning per ridurre le frodi
- Che cos’è la legge di Amdahl applicata all’elaborazione parallela
- Come creare un motore di raccomandazione con Python
- Come approcciare il problema del commesso viaggiatore
Come ordinare elementi con shell sort
L’algoritmo bubble sort confronta gli elementi vicini e li scambia se necessario. Se abbiamo una lista parzialmente ordinata, il bubble sort dovrebbe fornire prestazioni ragionevoli, poiché uscirà non appena non si verificherà più alcuno scambio di elementi in un ciclo.
Ma per una lista completamente non ordinata, di dimensioni N, possiamo dire che il bubble sort dovrà iterare completamente N – 1 passaggi per ordinarla completamente.
Donald Shell ha proposto l’ordinamento che da lui prende il nome, shell sort, chiedendosi se fosse il caso di selezionare gli elementi immediatamente vicini per le operazioni di confronto e scambio.
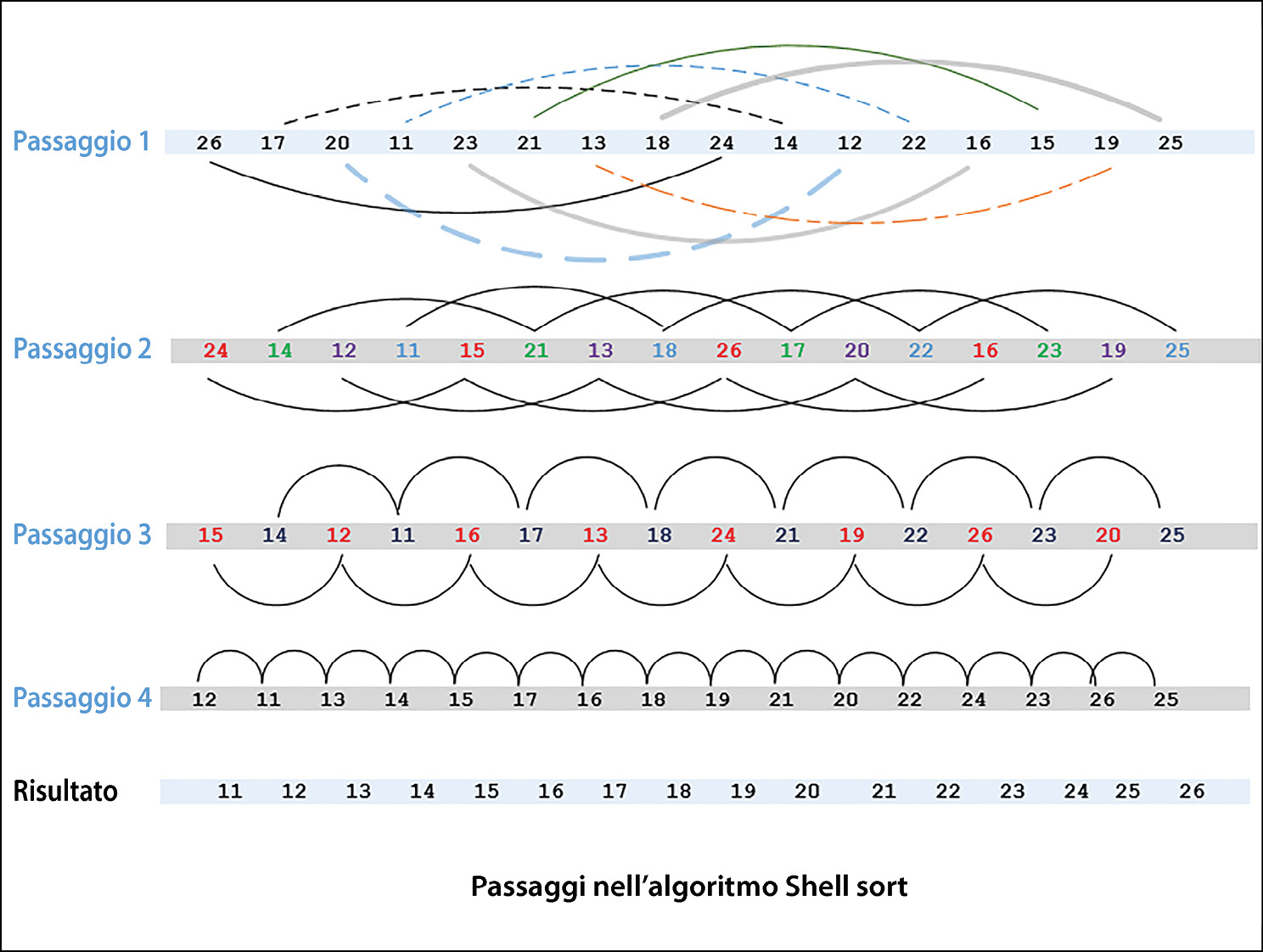
Ora, cerchiamo di capire questo concetto. Nel primo passaggio, invece di selezionare due elementi vicini, utilizziamo elementi che si trovano a un gap fisso, ordinando eventualmente una sottolista costituita da una coppia di punti. La situazione è mostrata nella prossima figura. Nel secondo passaggio, shell sort ordina sottoliste contenenti quattro elementi. Nei passaggi successivi, il numero di elementi per sottolista continua ad aumentare e il numero di sottoliste continua a diminuire, fino a raggiungere una situazione in cui c’è una sola sottolista costituita dall’intera lista di tutti gli elementi. A questo punto, possiamo supporre che la lista sia ordinata.
Come funziona shell sort.
In Python, il codice per implementare l’algoritmo di ordinamento di Shell è il seguente:
def ShellSort(list):
distance = len(list) // 2
while distance > 0:
for i in range(distance, len(list)):
temp = input_list[i]
j = i
# Ordina la sottolista per questa distanza
while j >= distance and list[j – distance] > temp:
list[j] = list[j – distance]
j = j-distance
list[j] = temp
# Riduce la distanza dall'elemento successivo
distance = distance// 2
return list
Il codice precedente può essere utilizzato per ordinare la lista:
Shell sort in azione.
Notiamo che la chiamata alla funzione ShellSort() produce l’ordinamento dell’array di input.
Analisi delle prestazioni di shell sort
Shell sort non è adatto ai big data, ma può essere utilizzato per dataset di medie dimensioni. In breve, offre prestazioni ragionevolmente buone su una lista con un massimo di 6.000 elementi, specialmente se i dati sono già parzialmente ordinati. Nel migliore dei casi, se una lista è già ordinata, sarà necessario un solo passaggio sugli N elementi per convalidare l’ordine, producendo una prestazione, nel migliore dei casi, pari a O(N).
Come usare il deep learning per ridurre le frodi
L’utilizzo di tecniche di machine learning per identificare documenti fraudolenti è un campo di ricerca attivo e stimolante. I ricercatori stanno studiando fino a che punto la capacità di riconoscimento dei pattern delle reti neurali può essere sfruttato per questo scopo. Invece di impiegare estrattori manuali di attributi, i pixel possono essere utilizzati per informare diverse architetture di deep learning.
Metodologia
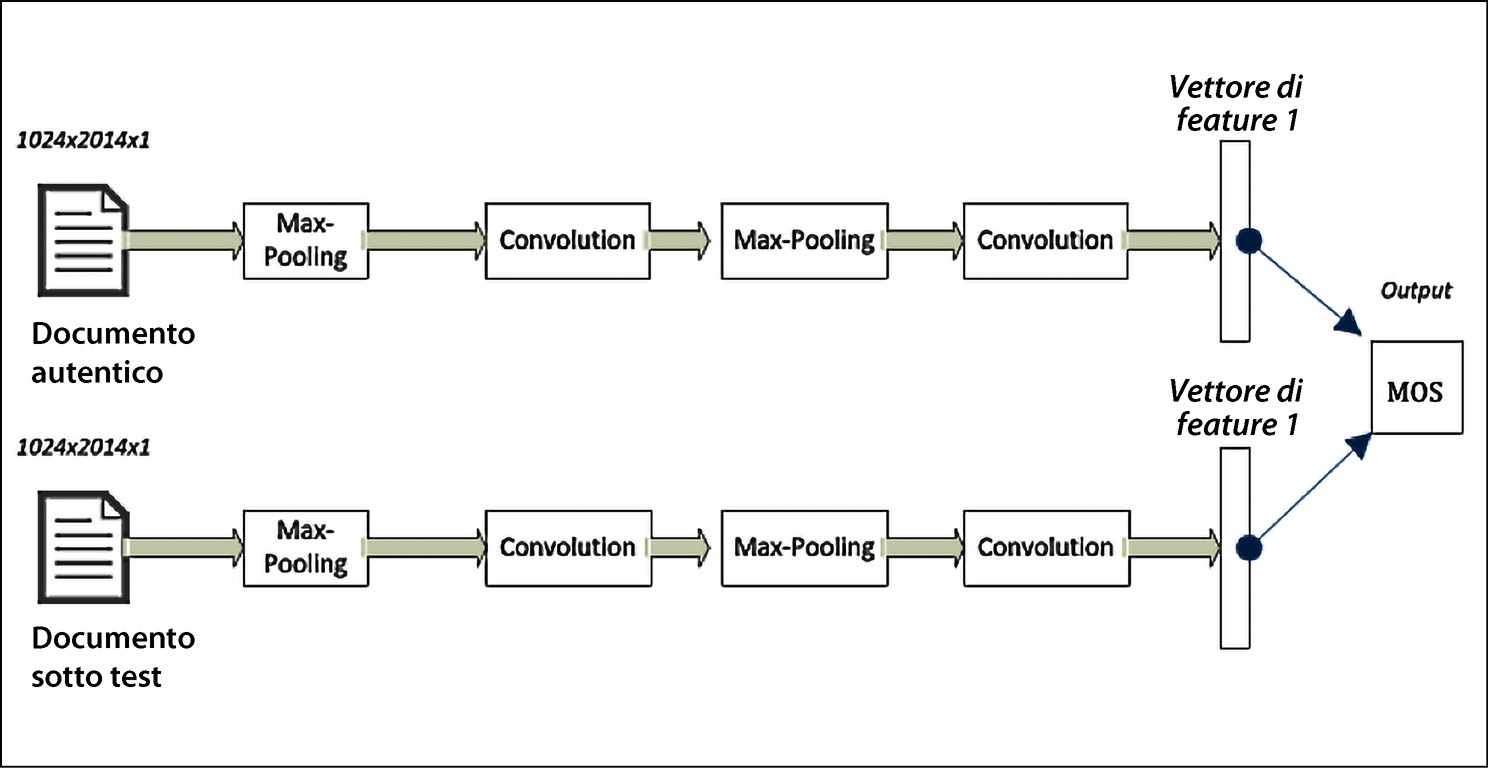
La tecnica presentata in questo paragrafo utilizza un’architettura a rete neurale chiamata reti neurali siamesi: due rami condividono architetture e parametri identici. L’uso di reti neurali siamesi per contrassegnare i documenti fraudolenti è rappresentato nella figura sottostante.
Architettura a reti neurali siamesi
Quando è necessario verificare l’autenticità di un determinato documento, prima classifichiamo il documento in base al suo layout e tipo; poi lo confrontiamo con i modelli e i pattern previsti. Se devia oltre una certa soglia, viene segnalato come falso; in caso contrario, è considerato un documento autentico, veritiero. Per casi d’uso critici, possiamo aggiungere un processo manuale nei casi in cui l’algoritmo non riesce a classificare in modo definitivo il documento come autentico o falso.
Per confrontare un documento con il modello previsto, utilizziamo due reti neurali convoluzionali identiche con un’architettura siamese. Le reti neurali convoluzionali hanno il vantaggio di individuare feature locali invarianti ottimali e possono costruire rappresentazioni resistenti alle distorsioni geometriche dell’immagine fornita in input. Si tratta quindi di un algoritmo adatto a questo problema, poiché puntiamo a far passare i documenti autentici e i documenti sotto test attraverso una singola rete, e quindi confrontare i risultati alla ricerca di somiglianze. Per raggiungere questo obiettivo, implementiamo i seguenti passaggi.
Supponiamo di voler sottoporre a test un documento. Per ogni classe di documento, eseguiamo questi passaggi.
- Leggere l’immagine archiviata del documento autentico. Lo chiamiamo documento autentico. Il documento sotto test dovrebbe avere l’aspetto del documento autentico.
- Il documento autentico viene fatto passare attraverso i layer della rete neurale per creare un vettore delle feature, che è la rappresentazione matematica dei pattern del documento autentico. È il vettore di feature 1 della figura precedente.
- Il documento di cui dobbiamo verificare l’autenticità è chiamato documento sotto test. Facciamo passare questo documento attraverso una rete neurale simile a quella utilizzata per creare il vettore delle feature del documento autentico. Il vettore delle feature del documento sotto test è chiamato vettore delle feature 2.
- Usiamo la distanza euclidea fra i due vettori delle feature per calcolare la somiglianza fra il documento autentico e il documento sotto test. Questo punteggio di somiglianza è chiamato Measure of Similarity (MOS) ed è un numero compreso fra 0 e 1. Un punteggio più alto rappresenta una minore distanza fra i documenti e quindi una maggiore probabilità che i documenti siano simili.
- Se il punteggio di somiglianza calcolato dalla rete neurale è inferiore a una certa soglia predefinita, contrassegnamo il documento come fraudolento.
Vediamo come possiamo implementare in Python queste reti neurali siamesi.
- Per prima cosa, importiamo i pacchetti Python richiesti:
import random
import numpy as npimport tensorflow as tf
- Successivamente, definiamo la rete neurale che verrà utilizzata per elaborare ciascuno dei rami della rete siamese:
def createTemplate():
return tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation = 'relu'),
tf.keras.layers.Dropout(0.15),
tf.keras.layers.Dense(128, activation = 'relu'),
tf.keras.layers.Dropout(0.15),
tf.keras.layers.Dense(64, activation = 'relu'),])
Notiamo che, al fine di contenere l’overfitting, ovvero il sovradattamento), abbiamo anche specificato un tasso
Dropoutpari a0,15. - Per implementare le reti siamesi, utilizzeremo le immagini MNIST (Modified National Institute of Standards and Technology), ideali per sottoporre a test l’efficacia del nostro approccio. Questo prevede la preparazione dei dati in modo tale che ogni campione abbia due immagini e un flag di somiglianza binaria, che è un indicatore che le due immagini appartengono alla stessa classe. Ora implementiamo la funzione
prepareData(), per preparare i dati:def prepareData(inputs: np.ndarray, labels: np.ndarray):
classesNumbers = 10
digitalIdx = [np.where(labels == i)[0] for i in range(classesNumbers)]
pairs = list()
labels = list()
n = min([len(digitalIdx[d]) for d in range(classesNumbers)]) – 1
for d in range(classesNumbers):
for i in range(n):
z1, z2 = digitalIdx[d][i], digitalIdx[d][i + 1]
pairs += [[inputs[z1], inputs[z2]]]
inc = random.randrange(1, classesNumbers)
dn = (d + inc) % classesNumbers
z1, z2 = digitalIdx[d][i], digitalIdx[dn][i]
pairs += [[inputs[z1], inputs[z2]]]
labels += [1, 0]return np.array(pairs), np.array(labels, dtype = np.float32)
Notate che
prepareData()produrrà un numero uguale di campioni per tutte le cifre. - Prepariamo i dataset di training e di test:
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train = x_train.astype(np.float32)
x_test = x_test.astype(np.float32)
x_train /= 255
x_test /= 255
input_shape = x_train.shape[1:]
train_pairs, tr_labels = prepareData(x_train, y_train)test_pairs, test_labels = prepareData(x_test, y_test)
- Ora creiamo le due metà del sistema siamese:
input_a = tf.keras.layers.Input(shape =input_shape)
enconder1 = base_network(input_a)
input_b = tf.keras.layers.Input(shape =input_shape)enconder2 = base_network(input_b)
- Quindi implementiamo la misura di similarità che quantificherà la distanza fra due documenti che vogliamo confrontare:
distance = tf.keras.layers.Lambda(lambda embeddings:
tf.keras.backend.abs(embeddings[0] – embeddings[1]))
([enconder1, enconder2])
measureOfSimilarity = tf.keras.layers.Dense(1, activation = 'sigmoid') (distance)
Infine, addestriamo il modello, in 10 “epoche” (epochs = 10):
Addestramento del modello, in dieci epoche.
Notiamo che abbiamo raggiunto una precisione del 97,49% utilizzando 10 epoche. Un aumento del numero di epoche migliorerà ulteriormente il livello di precisione.
Leggi anche: Introduzione al Quantum Computing, di Marco Ivaldi
Che cos’è la legge di Amdahl applicata all’elaborazione parallela
Gene Amdahl è stato uno dei primi a studiare l’elaborazione parallela negli anni sessanta, quando sviluppò la legge di Amdahl, che ancora oggi è applicabile e può fungere da base per comprendere i vari compromessi legati alla progettazione di una soluzione di calcolo parallelo. La legge di Amdahl può essere spiegata come segue.
Si basa sul concetto che in qualsiasi processo informatico, non tutti i processi possono essere eseguiti in parallelo. Ci sarà sempre una parte sequenziale del processo che non può essere parallelizzata.
Vediamo un esempio: supponiamo di voler leggere un numero elevato di file archiviati su un computer e di voler addestrare un modello di machine learning utilizzando i dati trovati in questi file.
L’intero processo è chiamato P. È ovvio che P può essere suddiviso nei due sottoprocessi seguenti:
- P1 scansiona i file nella directory, crea una lista di nomi di file che corrispondono al file di input e li passa avanti;
- P2 legge i file, crea la pipeline di elaborazione dati, elabora i file e addestra il modello.
Condurre l’analisi di processi sequenziali
Il tempo per eseguire P è rappresentato da Tseq(P ). I tempi per eseguire P1 e P2 sono rappresentati da Tseq(P1) e Tseq(P2). È ovvio che, quando disponiamo di un solo nodo, possiamo osservare due cose:
- P2 non può iniziare a funzionare prima che P1 sia completo. Questo è rappresentato da P1 –> P2;
- Tseq(P ) = Tseq(P1) + Tseq(P2)
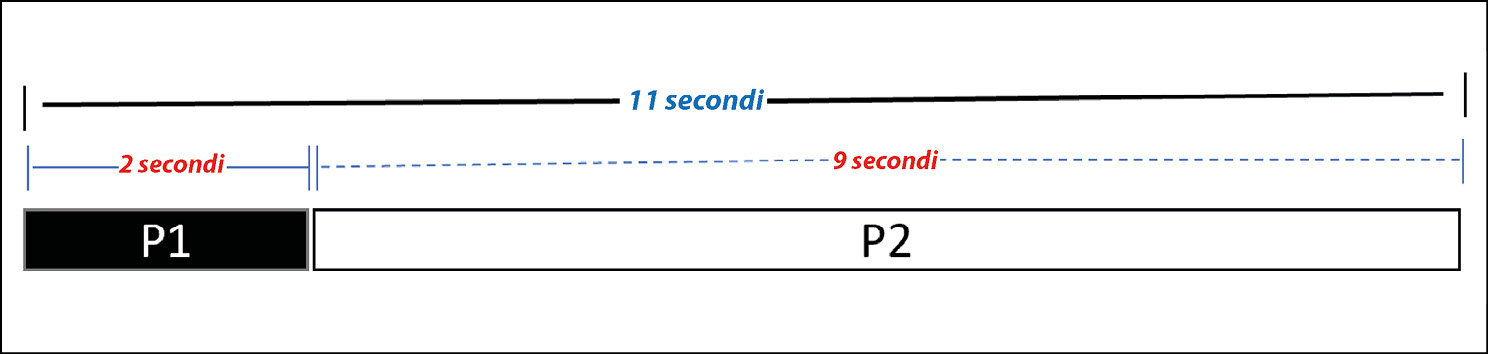
Supponiamo che P impieghi complessivamente 11 minuti per essere eseguito su un singolo nodo. Di questi 11 minuti, P1 impiega 2 minuti e P2 impiega 9 minuti. Ciò è rappresentato nella figura qui sotto.
La legge di Amdahl applicata all’elaborazione parallela.
Ora la cosa importante da notare è che P1 ha una natura sequenziale. Non possiamo far sì che sia più veloce rendendolo parallelo. Al contrario, P2 può essere facilmente suddiviso in più attività che possono essere eseguite in parallelo. Quindi, possiamo accelerare questo processo dell’algoritmo eseguendolo in parallelo.
La legge di Amdahl e il cloud
Il principale vantaggio dell’utilizzo del cloud computing è la disponibilità di un ampio pool di risorse e dal loro utilizzo in parallelo. Il piano per utilizzare queste risorse per risolvere un determinato problema è chiamato piano di esecuzione. La legge di Amdahl viene utilizzata per identificare i colli di bottiglia dato un problema e un pool di risorse per risolverlo.
Come creare un motore di raccomandazione con Python
Costruiamo un motore di raccomandazione in grado di consigliare film a un gruppo di utenti. Useremo i dati raccolti dal gruppo di ricerca GroupLens Research presso l’università del Minnesota.
- Innanzitutto, dobbiamo importare i pacchetti necessari:
import pandas as pd import numpy as np - Ora, importiamo i dataset:
df_reviews = pd.read_csv('reviews.csv') df_movie_titles = pd.read_csv('movies.csv', index_col= False) - Uniamo i due DataFrame in base a
movieID:df = pd.merge(df_users, df_movie_titles, on = 'movieId')
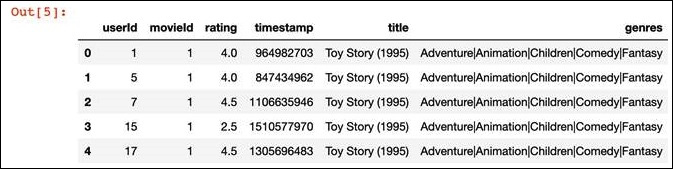
L’intestazione del DataFrame
df, dopo aver eseguito il codice precedente, ha il seguente aspetto:L’intestazione del DataFrame.
I dettagli delle colonne sono i seguenti.
userid: l’ID univoco di ciascun utente.movieid: l’ID univoco di ciascun film.rating: le valutazioni dei film, da 1 a 5.timestamp: il timestamp in cui il film è stato valutato.title: il titolo del film.genres: il genere del film.
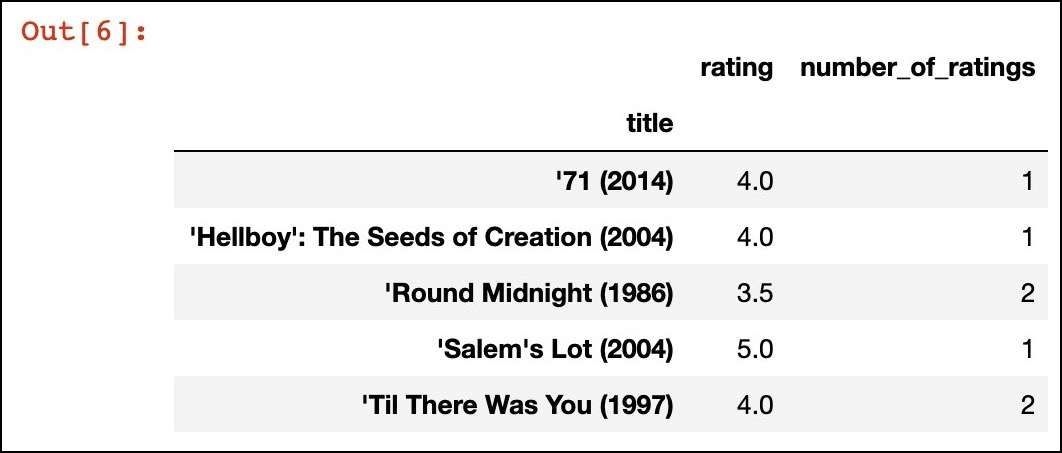
- Per esaminare le tendenze nei dati di input, calcoliamo la media e il conteggio delle valutazioni per film, utilizzando
groupbyper le colonnetitleerating:Calcoliamo la media e il conteggio delle valutazioni per ogni film.
- Ora prepariamo i dati per il motore di raccomandazione. Per farlo, trasformeremo il dataset in una matrice, che avrà le seguenti caratteristiche:
- le colonne saranno i titoli dei film;
- l’indice sarà
userid; - il valore sarà
rating.
Useremo la funzione
pivot_table()di DataFrame:movie_matrix = df.pivot_table(index= 'userId', columns = 'title', values = 'rating')
Questa riga di codice genererà una matrice molto sparsa.
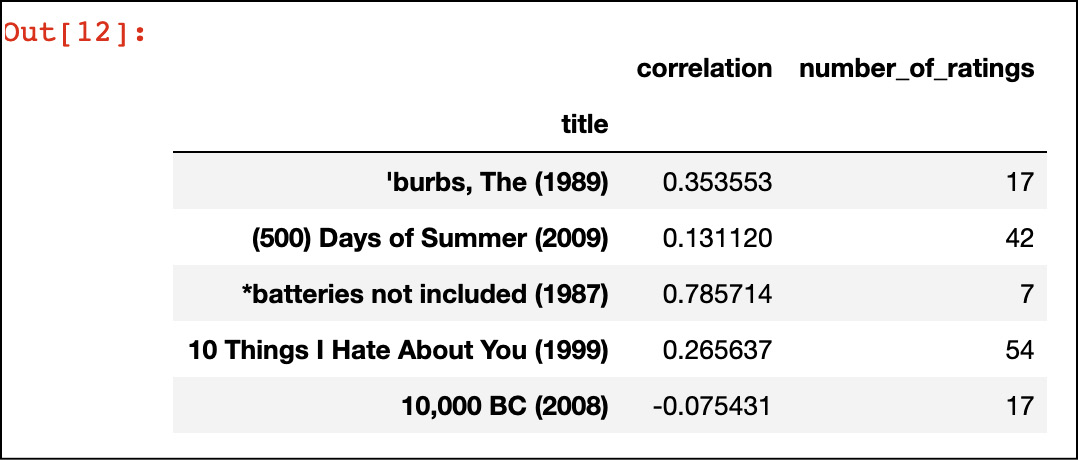
- Ora usiamo la matrice di raccomandazioni che abbiamo creato per consigliare i film. Per farlo, consideriamo un determinato utente che ha visto il film, Avatar (2009). Innanzitutto, troviamo tutti gli utenti che hanno mostrato interesse per Avatar (2009):
Avatar_user_rating = movie_matrix['Avatar (2009)']
Avatar_user_rating = Avatar_user_rating.dropna() Avatar_user_rating.head() - Ora proviamo a suggerire i film correlati ad Avatar (2009). Per farlo, calcoleremo la correlazione fra il DataFrame
Avatar_user_ratingconmovie_matrix, come segue:
similar_to_Avatar =movie_matrix.corrwith(Avatar_user_rating)
corr_Avatar = pd.DataFrame(similar_to_Avatar,
columns = ['correlation'])
corr_Avatar.dropna(inplace = True)
corr_Avatar = corr_Avatar.join(df_ratings['number_of_ratings'])
corr_Avatar.head()
Otterremo il seguente output:
Film che possiamo suggerire all’utente in base alla valutazione compiuta dall’algoritmo.
Ciò significa che possiamo suggerire questi film all’utente.
Come approcciare il problema del commesso viaggiatore
Esaminiamo, innanzitutto, la dichiarazione del problema del commesso viaggiatore, ideato come sfida negli anni Trenta. Si tratta di un problema NP-difficile. Per cominciare, possiamo generare casualmente un percorso che soddisfi la condizione di visitare tutte le città senza preoccuparci di quale sia la soluzione ottimale e poi possiamo lavorare per cercare di migliorare la soluzione a ogni iterazione.
Ogni percorso generato in un’iterazione è chiamato soluzione candidata (chiamato un certificato). Dimostrare che un certificato è ottimale richiede una quantità di tempo esponenzialmente crescente. Al contrario, utilizziamo diverse soluzioni basate su euristiche per generare percorsi prossimi a quello ottimale, ma non ottimali.
Un commesso viaggiatore deve visitare un determinato elenco di città per svolgere il proprio lavoro:
| INPUT | Una lista di n città (denotata con V) e le distanze d fra le varie coppie di città d(i, j) con 1 ≤ i ≤ n e 1 ≤ j ≤ n). | ||
| OUTPUT | Il percorso più breve che visita ciascuna città esattamente una volta e poi torna alla città iniziale. |
Notiamo quanto segue:
- sono note le distanze fra le città della lista;
- ogni città dell’elenco fornito deve essere visitata esattamente una volta.
Possiamo generare il piano per il commesso viaggiatore? Quale sarà la soluzione ottimale in grado di ridurre al minimo la distanza totale da lui percorsa?
Le seguenti sono le distanze fra cinque città canadesi, che possiamo utilizzare per il problema del commesso viaggiatore:
| Ottawa | Montreal | Kingston | Toronto | Sudbury | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ottawa | – | 199 | 196 | 450 | 484 | ||||||
| Montreal | 199 | – | 287 | 542 | 680 | ||||||
| Kingston | 196 | 287 | – | 263 | 634 | ||||||
| Toronto | 450 | 542 | 263 | – | 400 | ||||||
| Sudbury | 484 | 680 | 634 | 400 | – |
Notate che l’obiettivo è quello di ottenere un percorso che parta e arrivi nella città iniziale. Per esempio, un percorso tipico può essere Ottawa – Sudbury – Montreal – Kingston – Toronto – Ottawa con un costo pari a 484 + 680 + 287 + 263 + 450 = 2.164. È questo il percorso in cui il commesso viaggiatore percorre la distanza minima? Quale sarà la soluzione ottimale in grado di ridurre al minimo la distanza totale percorsa dal commesso viaggiatore? Lascio a chi legge il compito di riflettere e calcolarla.
Usare una strategia a forza bruta
La prima soluzione che viene in mente per risolvere il problema del commesso viaggiatore è quella di usare la forza bruta per trovare il percorso più breve con cui il commesso viaggiatore può visitare ogni città esattamente una volta e tornare alla città da cui è partito. La strategia a forza bruta funziona come segue.
- Valutare tutti i percorsi possibili.
- Scegliere quello per il quale otteniamo la distanza più breve.
Il problema è che per n città ci sono (n – 1)! possibili percorsi. Ciò significa che cinque città produrranno 4! = 24 percorsi e selezioneremo quello che corrisponde alla distanza più breve. È ovvio che questo metodo funzionerà solo perché non abbiamo troppe città. All’aumentare del numero di città, la strategia a forza bruta diventa impraticabile, a causa del gran numero di permutazioni generate utilizzando questo approccio.
Vediamo come possiamo implementare la strategia a forza bruta in Python.
Innanzitutto, notiamo che {1, 2, 3} rappresenta un percorso dalla città 1 alla città 2 alla città 3. La distanza totale di un percorso è la somma delle distanze percorse. Supporremo che la distanza fra le città sia semplicemente la distanza in linea d’aria (la distanza euclidea).
Definiamo prima tre funzioni di servizio.
distance_points(): calcola la distanza assoluta fra due punti.distance_tour(): calcola la distanza totale che il commesso viaggiatore deve percorrere per coprire un determinato percorso.generate_cities(): genera casualmente un insieme di n città situate in un rettangolo di larghezza500e altezza300.
Esaminiamo il seguente codice:
import random
from itertools import permutations
alltours = permutations
def distance_tour(aTour):
return sum(distance_points(aTour[i – 1], aTour[i])
for i in range(len(aTour)))
aCity = complex
def distance_points(first, second): return abs(first – second)
def generate_cities(number_of_cities):
seed = 111; width = 500; height = 300
random.seed((number_of_cities, seed))
return frozenset(aCity(random.randint(1, width), random.randint(1, height))
for c in range(number_of_cities))
Nel codice precedente, abbiamo implementato alltours con la funzione permutations del pacchetto itertools. Abbiamo anche rappresentato la distanza con un numero complesso. Ciò significa quanto segue.
- Il calcolo della distanza fra due città,
aeb, èdistance(a, b). - Possiamo creare n città semplicemente richiamando
generate_cities(n).
Definiamo ora una funzione brute_force() che generi tutti i percorsi fra le città. Una volta generati tutti i percorsi possibili, sceglierà quello con la distanza più breve:
def brute_force(cities):
"Generiamo tutti gli itinerari possibili e scegliamo il più corto."
return shortest_tour(alltours(cities))
def shortest_tour(tours): return min(tours, key = distance_tour)
Definiamo ora le funzioni di servizio in grado di aiutarci a tracciare le città.
visualize_tour(): traccia tutte le città e i collegamenti di un determinato percorso. Evidenzia anche la città da cui è iniziato il percorso.visualize_segment(): utilizzata davisualize_tour()per tracciare le città e i singoli collegamenti.
Osservate il seguente codice:
%matplotlib inline
import matplotlib.pyplot as plt
def visualize_tour(tour, style = 'bo-'):
if len(tour) > 1000: plt.figure(figsize = (15, 10))
start = tour[0:1]
visualize_segment(tour + start, style)
visualize_segment(start, 'rD')
def visualize_segment(segment, style = 'bo-'):
plt.plot([X(c) for c in segment], [Y(c) for c in segment], style, clip_on = False)
plt.axis('scaled')
plt.axis('off')
def X(city): "X axis"; return city.real
def Y(city): "Y axis"; return city.imag
Implementiamo la funzione tsp() che fa quanto segue.
- Genera il percorso in base all’algoritmo e al numero di città richieste.
- Calcola il tempo impiegato dall’algoritmo per l’esecuzione.
- Genera un tracciato.
Una volta definita tsp(), possiamo usarla per tracciare un percorso:
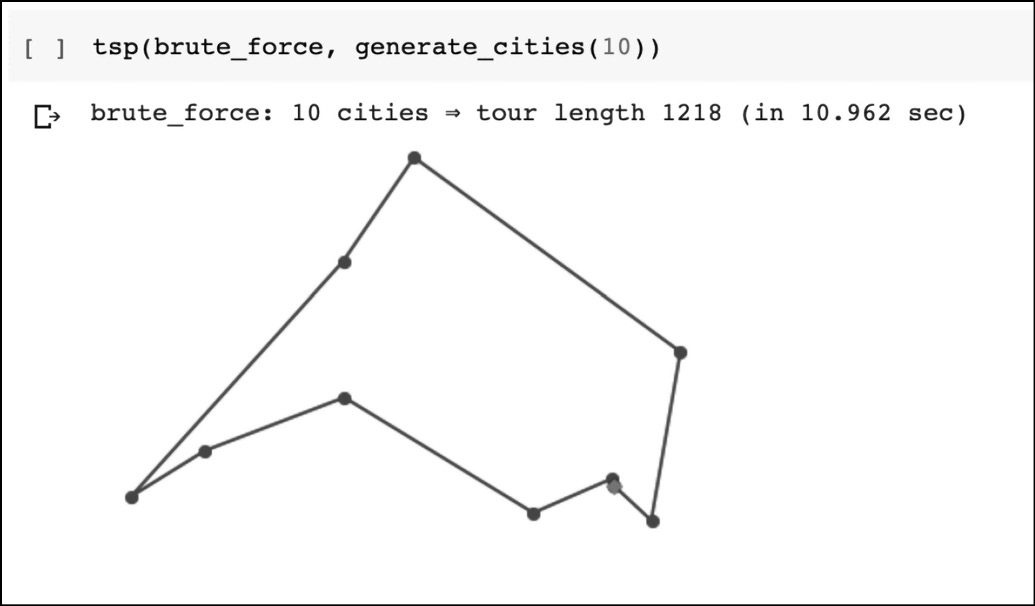
Programmiamo il percorso del commesso viaggiatore.
Il risultato del percorso del commesso viaggiatore.
Notiamo che l’abbiamo usata per generare il percorso per dieci città. Poiché n = 10, genererà (10 – 1)! = 362.880 possibili permutazioni. Al crescere di n, il numero di permutazioni cresce enormemente e il metodo della forza bruta diviene impraticabile.
Usare un algoritmo greedy
Se usiamo un algoritmo greedy per risolvere il problema del commesso viaggiatore, allora, a ogni passo, possiamo scegliere una città che ci sembra ragionevole, invece di trovare quella città che produrrà il miglior percorso in assoluto. Quindi, ogni volta che dobbiamo selezionare una città, selezioniamo semplicemente la città più vicina, senza preoccuparci di verificare che questa scelta produca il percorso ottimale.
L’approccio dell’algoritmo greedy è semplice.
- Partiamo da qualsiasi città.
- A ogni passaggio, continuiamo a costruire il percorso spostandoci nella città più vicina che non è stata ancora visitata.
- Ripetiamo il Passaggio 2.
Definiamo una funzione greedy_algorithm() per implementare questa logica:
def greedy_algorithm(cities, start = None):
C = start or first(cities)
tour = [C] unvisited = set(cities – {C})
while unvisited:
C = nearest_neighbor(C, unvisited)
tour.append(C)
unvisited.remove(C)
return tour
def first(collection): return next(iter(collection))
def nearest_neighbor(A, cities):
return min(cities, key = lambda C: distance_points(C, A))
Ora usiamo greedy_algorithm() per creare un percorso per 2.000 città:
Un algoritmo greedy affronta il problema del commesso viaggiatore.
Notiamo che ci sono voluti solo 0,514 secondi per generare il percorso per 2.000 città. Il metodo della forza bruta avrebbe dovuto generare (2000 – 1)! permutazioni, che è un numero quasi infinito.
Notiamo che l’algoritmo greedy si basa sull’euristica e non ci sono prove che la soluzione che fornisce sarà ottimale.
Questo articolo richiama contenuti da 40 algoritmi che ogni programmatore deve conoscere.
Immagine di apertura di Fotis Fotopoulos su Unsplash.