Che cos’è un algoritmo e come progettarlo

Che cos’è un algoritmo

In breve, un algoritmo è un insieme di regole per eseguire i calcoli necessari per risolvere un problema. Un algoritmo è progettato per fornire risultati per qualsiasi input valido, secondo istruzioni definite con precisione. Cercando la definizione di algoritmo in un dizionario come l’American Heritage, si trova che:

Un algoritmo è un insieme finito di istruzioni non ambigue che, dato un insieme di condizioni iniziali, può essere eseguito secondo una sequenza prescritta per raggiungere un determinato obiettivo e che ha un insieme riconoscibile di condizioni finali.

La progettazione di un algoritmo tenta di creare una ricetta matematica del modo più efficiente per risolvere un determinato problema concreto. Questa ricetta può essere utilizzata come base per sviluppare una soluzione matematica riutilizzabile e generica, che possa essere applicata a un insieme più ampio di problemi simili.

Le fasi di un algoritmo

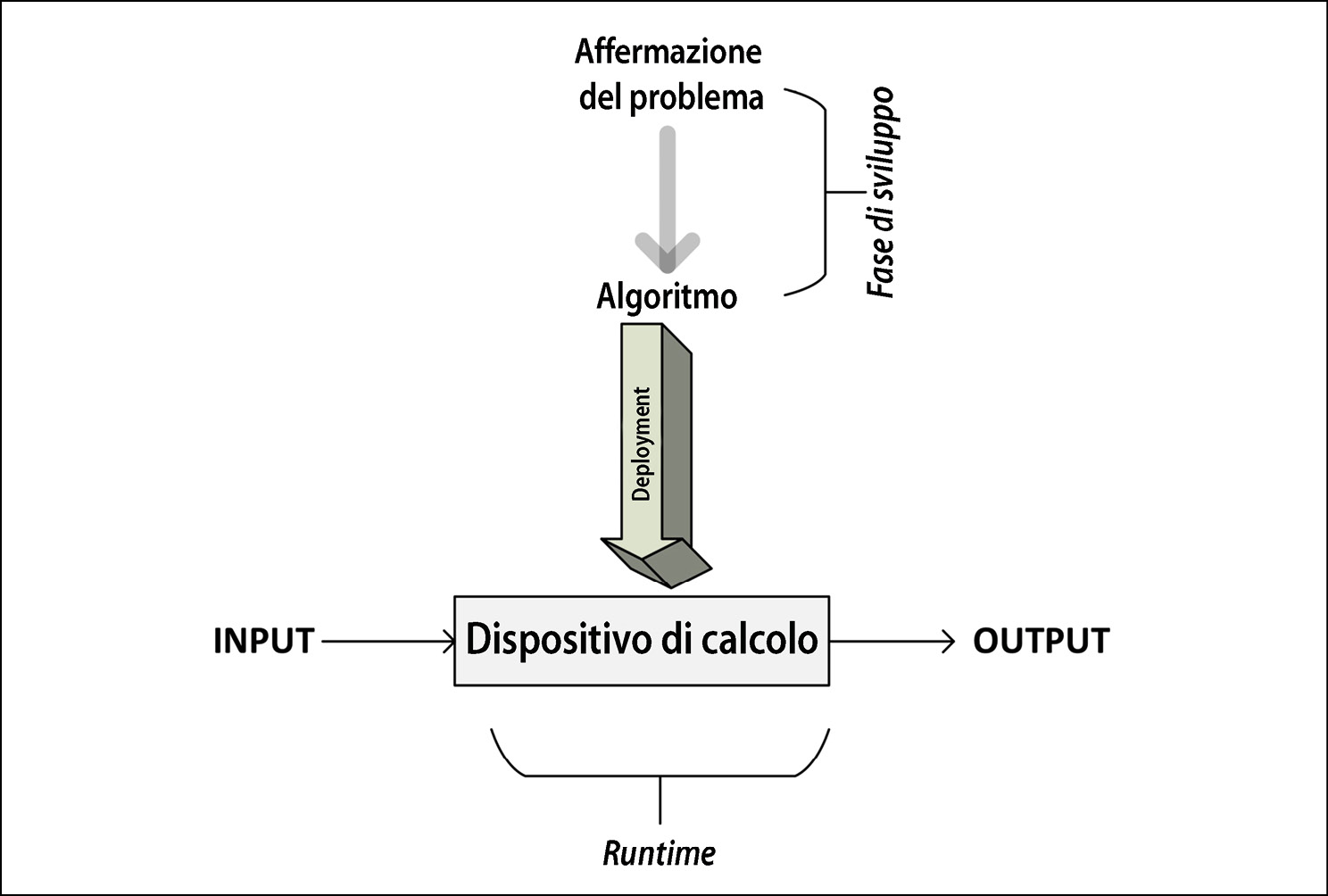
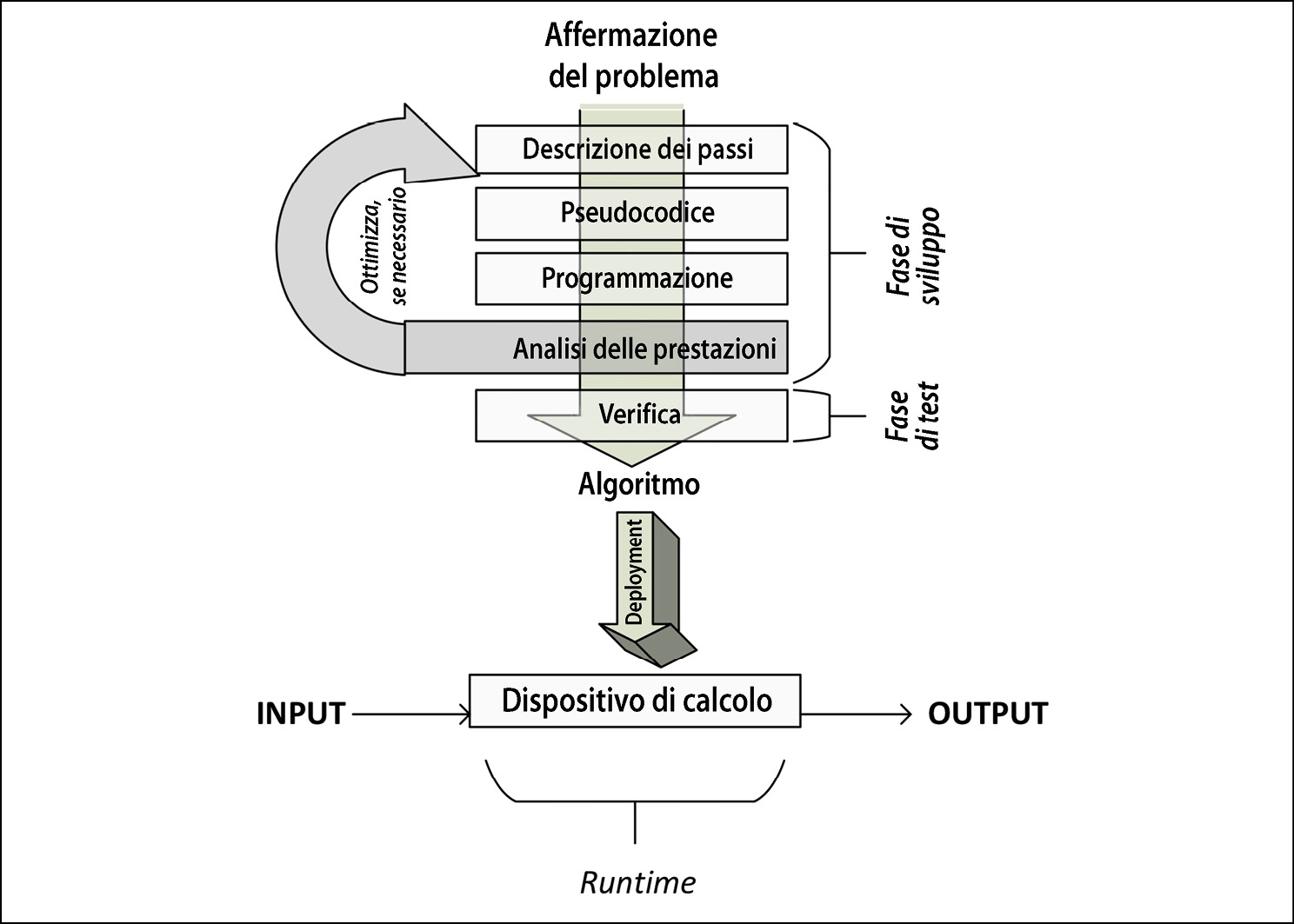
La prossima figura mostra le diverse fasi di sviluppo, implementazione e utilizzo di un algoritmo.

Le diverse fasi di sviluppo, implementazione e utilizzo di un algoritmo.

Come possiamo vedere, il processo inizia con la comprensione dei requisiti, dall’affermazione del problema, che specificano quale risultato occorre ottenere. Una volta che il problema è esposto chiaramente, si passa alla fase di sviluppo.

La fase di sviluppo di un algoritmo si compone a sua volta di due fasi.

• La fase di progettazione, durante la quale vengono immaginati e documentati l’architettura, la logica e i dettagli di implementazione dell’algoritmo. In questa fase teniamo presente sia l’accuratezza sia le prestazioni. Durante la ricerca della soluzione per un dato problema, in molti casi finiremo per avere più algoritmi alternativi. La fase di progettazione di un algoritmo è un processo iterativo, che prevede il confronto di diversi algoritmi candidati. Alcuni algoritmi possono fornire soluzioni semplici e veloci, ma a scapito della precisione. Altri algoritmi possono essere molto accurati, ma la loro esecuzione può richiedere molto tempo, a causa della loro complessità. Alcuni di questi algoritmi complessi possono essere più efficienti di altri. Prima di effettuare una scelta, occorre studiare attentamente tutti i compromessi intrinseci degli algoritmi candidati. Soprattutto se il problema è complesso, è molto importante progettare un algoritmo efficiente. Un algoritmo progettato correttamente si tradurrà in una soluzione efficiente che sarà in grado di fornire, allo stesso tempo, prestazioni soddisfacenti e un’accuratezza ragionevole.
• La fase di programmazione, durante la quale l’algoritmo progettato viene convertito in un programma. È importante che tale programma implementi tutte le logiche e le architetture suggerite in fase di progettazione.

Una volta progettato e implementato in un linguaggio di programmazione a scelta, il codice dell’algoritmo è pronto per essere distribuito. La distribuzione (deployment) di un algoritmo coinvolge la progettazione dell’ambiente di produzione in cui verrà effettivamente eseguito il codice. L’ambiente di produzione deve essere progettato in base ai dati e alle esigenze elaborative dell’algoritmo. Per esempio, per algoritmi parallelizzabili, per l’esecuzione efficiente dell’algoritmo sarà necessario prevedere un cluster con un numero appropriato di nodi di calcolo. Per gli algoritmi a elevata intensità di dati, potrebbe essere necessario progettare una pipeline di ingresso dei dati e una strategia per memorizzare in cache e archiviare i dati. Una volta che l’ambiente di produzione è stato progettato e implementato, l’algoritmo viene distribuito e inizia ad accettare i dati di input, a elaborarli e a generare l’output, secondo i requisiti.

La logica di un algoritmo

Quando si progetta un algoritmo, è importante trovare modi diversi per specificarne i dettagli, curando la capacità di catturarne sia la logica sia l’architettura. In generale, proprio come quando si costruisce una casa, è importante specificare la struttura di un algoritmo, prima di implementarlo effettivamente. Per algoritmi più complessi e distribuiti, la pianificazione preliminare del modo in cui la loro logica sarà distribuita nel cluster per l’esecuzione è importante per guidare in modo efficiente il processo iterativo di progettazione. Attraverso lo pseudocodice e i piani di esecuzione, entrambe queste esigenze vengono soddisfatte, come vedremo nel prossimo paragrafo.

Che cos’è lo pseudocodice

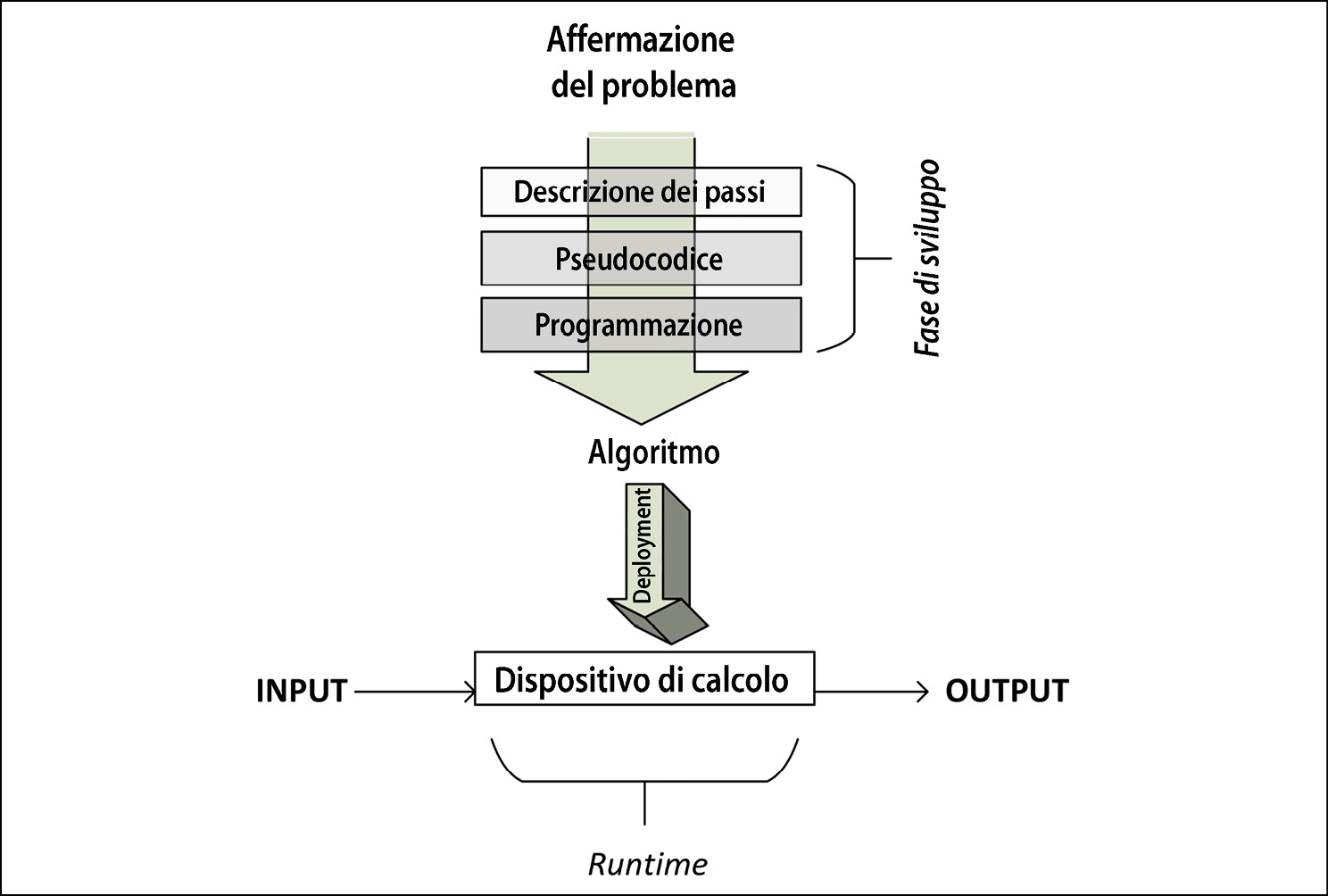
Il modo più semplice per specificare la logica di un algoritmo consiste nello scriverne una descrizione di alto livello in un modo semistrutturato, chiamato pseudocodice. Prima di scrivere in pseudocodice la logica di un algoritmo, è utile descriverne il flusso principale scrivendo i passaggi principali in linguaggio naturale. Poi, questa descrizione testuale deve essere convertita in pseudocodice, che rappresenta un modo strutturato per scrivere questa descrizione in modo che essa rappresenti più rigorosamente la logica e il flusso dell’algoritmo. Lo pseudocodice dell’algoritmo, se ben scritto, deve descrivere ad alto livello i passaggi dell’algoritmo stesso, con un livello di dettaglio ragionevole, perché se eccessivo non è particolarmente rilevante per descrivere il flusso principale e la struttura. La figura seguente mostra il flusso dei passaggi.

Una volta scritto lo pseudocodice, siamo pronti per programmare l’algoritmo.

Notiamo che, una volta scritto lo pseudocodice (come vedremo nel prossimo paragrafo), siamo pronti per programmare l’algoritmo utilizzando un linguaggio a scelta.

Un esempio pratico di pseudocodice

Di seguito si può vedere lo pseudocodice di un algoritmo di allocazione delle risorse, chiamato SRPMP. Nel cluster computing, ci sono molte situazioni in cui più attività parallele devono essere eseguite su un dato insieme di risorse disponibili, chiamate collettivamente pool di risorse. Questo algoritmo assegna le attività a una risorsa e crea una mappatura, chiamata Ω. Notate che questo pseudocodice cattura la logica e il flusso dell’algoritmo, elementi che verranno meglio spiegati di seguito.

1: BEGIN Mapping_Phase
     2: Ω = { }
     3: k = 1
     4: FOREACH Ti∈T
     5:     ωi = RA(∆k, Ti)
     6:     add {ωi, Ti} to Ω
     7:     state_changeTi [STATE 0: Idle/Unmapped] → [STATE 1: Idle/Mapped]
     8:     k=k+1
     9:     IF (k>q)
    10:         k= 1
    11:     ENDIF
    12: END FOREACH
    13: END Mapping_Phase

Analizziamo questo algoritmo riga per riga.

1. Avviamo la mappatura eseguendo l’algoritmo. Il set di mappatura Ω è vuoto.
2. Viene selezionata la prima partizione come pool di risorse per l’attività T1 (vedi la riga 3 del codice precedente). Television Rating Point (TRPS) richiama in modo iterativo l’algoritmo per l’artrite reumatoide (Reumatoid Arthritis, RA) per ogni attività Ti con una delle partizioni scelte come pool di risorse.
3. L’algoritmo RA restituisce l’insieme delle risorse scelte per l’attività Ti, rappresentato da ωi (vedi riga 5 del codice precedente).
4. Ti e ωi vengono aggiunti al set di mappatura (vedi riga 6 del codice precedente).
5. Lo stato di Ti viene modificato da STATE 0: Idle/Unmapped a STATE 1: Idle/Mapped (vedi riga 7 del codice precedente).
6. Notiamo che per la prima iterazione k = 1 e viene selezionata la prima partizione. Per ogni successiva iterazione, il valore di k aumenta fino a che k > q.
7. Se k diventa maggiore di q, viene riportato a 1 (vedi righe 9 e 10 del codice precedente).
8. Questo processo si ripete finché non viene determinata una mappatura fra tutte le attività e l’insieme di risorse che utilizzeranno e tale mappatura memorizzata in un insieme di mappatura chiamato Ω.
9. Una volta che ciascuna delle attività è mappata su un insieme di risorse nella fase di mappatura, l’attività viene eseguita.

Leggi anche: Machine Learning: accedere alle recenzioni di IMDB, di Sebastian Raschka

Utilizzo degli snippet

Con la crescita di popolarità di un linguaggio di programmazione semplice ma potente come Python, si sta diffondendo sempre più un approccio alternativo, che consiste nel rappresentare la logica dell’algoritmo direttamente nel linguaggio di programmazione, seppure in una versione un po’ semplificata. Come lo pseudocodice, questo codice cattura la logica di base e la struttura dell’algoritmo, evitando di entrare troppo nei dettagli. Questo tipo di codice è chiamato anche snippet. Per esempio, esaminiamo un semplice snippet relativo a una funzione Python che può essere utilizzata per scambiare due variabili:

define swap(x, y)
        buffer = x
        x = y
        y = buffer

Creazione di un piano di esecuzione

Non sempre una descrizione in pseudocodice e sotto forma di snippet è sufficiente per chiarire tutta la logica relativa agli algoritmi distribuiti più complessi. Per esempio, in genere gli algoritmi distribuiti devono essere suddivisi runtime in più fasi, in base a un ordine di precedenza. La giusta strategia per suddividere il problema, in tutta la sua ampiezza, in un numero ottimale di fasi con i giusti vincoli di precedenza è cruciale per l’esecuzione efficiente di un algoritmo.

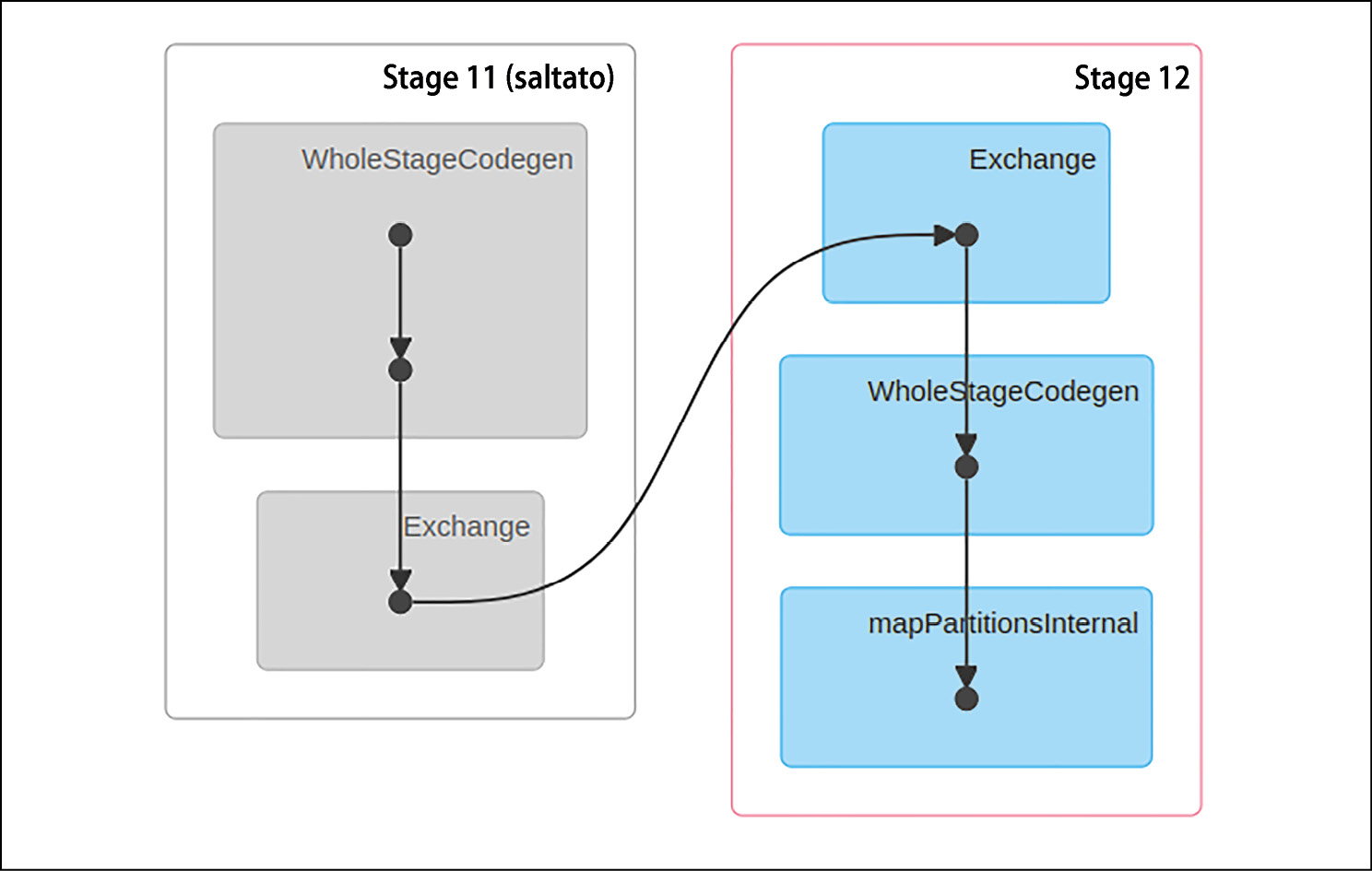
Dobbiamo trovare un modo per rappresentare anche questa strategia per riuscire a rappresentare appieno la logica e la struttura di un algoritmo. Un piano di esecuzione è uno dei metodi usati per dettagliare il modo in cui l’algoritmo verrà suddiviso in un gruppo di attività. Un’attività può essere costituita da mappatori o riduttori, i quali possono essere raggruppati in blocchi, chiamati fasi, stage. La figura qui di seguito mostra un piano di esecuzione generato da un runtime Apache Spark prima dell’esecuzione di un algoritmo. Descrive in dettaglio le attività runtime in cui sarà suddiviso il job creato per l’esecuzione dell’algoritmo stesso.

Notiamo che la figura prevede cinque attività, divise in due diverse fasi, denominate Stage 11 e Stage 12.

Le cinque attività all’interno del piano di esecuzione di un algoritmo.

Tecniche di progettazione degli algoritmi

Un algoritmo è una soluzione matematica a un problema concreto. Quando progettiamo un algoritmo, teniamo a mente i seguenti tre problemi di progettazione.

1. Questo algoritmo sta producendo il risultato che ci aspettavamo?
2. Questo algoritmo rappresenta il modo ottimale per ottenere questi risultati?
3. Come funzionerà l’algoritmo su dataset di maggiori dimensioni?

È importante studiare a fondo la complessità del problema, prima di progettarne una soluzione. Per esempio, per progettare una soluzione adeguata è utile caratterizzare il problema in termini di sue esigenze e complessità. In generale, gli algoritmi possono essere suddivisi nelle seguenti tipologie, in base alle caratteristiche del problema.

• Algoritmi a elevata intensità di dati (data-intensive): sono progettati per gestire grandi quantità di dati. Ci si aspetta che abbiano requisiti di elaborazione relativamente ridotti. Un algoritmo di compressione applicato a un file enorme è un buon esempio di algoritmo a elevata intensità di dati. Per tali algoritmi, la dimensione dei dati gestibili dovrebbe essere molto maggiore della memoria del sistema di elaborazione (il singolo nodo o l’intero cluster) e, in base ai requisiti, potrebbe essere necessario adottare uno schema di elaborazione iterativo per poter elaborare in modo efficiente i dati.
• Algoritmi a elevata intensità di calcoli (compute-intensive): hanno requisiti di elaborazione considerevoli, ma non elaborano grandi quantità di dati. Un semplice esempio è l’algoritmo per trovare un numero primo molto grande. Per massimizzare le prestazioni dell’algoritmo è fondamentale trovare una strategia per suddividere l’algoritmo in più fasi, in modo che almeno alcune di esse possano essere parallelizzate.
• Algoritmi a elevata intensità di dati e di calcoli: esistono alcuni algoritmi che si trovano a gestire una grande quantità di dati ma hanno anche notevoli requisiti di in termini di elaborazione. Gli algoritmi utilizzati per eseguire l’analisi del sentiment per i feed video in diretta sono un buon esempio di situazioni in cui sia i dati sia i requisiti di elaborazione sono enormi, per poter portare a termine l’attività. Questi sono gli algoritmi più dispendiosi in termini di risorse e richiedono un’attenta progettazione e un’allocazione intelligente delle risorse disponibili.

Per caratterizzare il problema in termini di complessità e requisiti, è utile studiare i dati e calcolare le dimensioni in modo più approfondito, cosa che faremo nel prossimo paragrafo.

La dimensione dei dati

Per classificare la dimensione dei dati del problema, osserviamo il loro volume, la loro velocità e la loro varietà (le tre “V”), che sono definite come segue.

• Volume: è la dimensione fisica prevista dei dati che l’algoritmo dovrà elaborare: MB, GB, TB, PB…
• Velocity: è la rapidità con la quale vengono generati nuovi dati quando viene utilizzato l’algoritmo. Può essere pari a zero, nel caso delle attività batch, ma può essere periodica, near real-time o real-time.
• Variety: descrive quanti diversi tipi di dati l’algoritmo si troverà a elaborare: precise tabelle, dati NoSQL o dati completamente non strutturati.

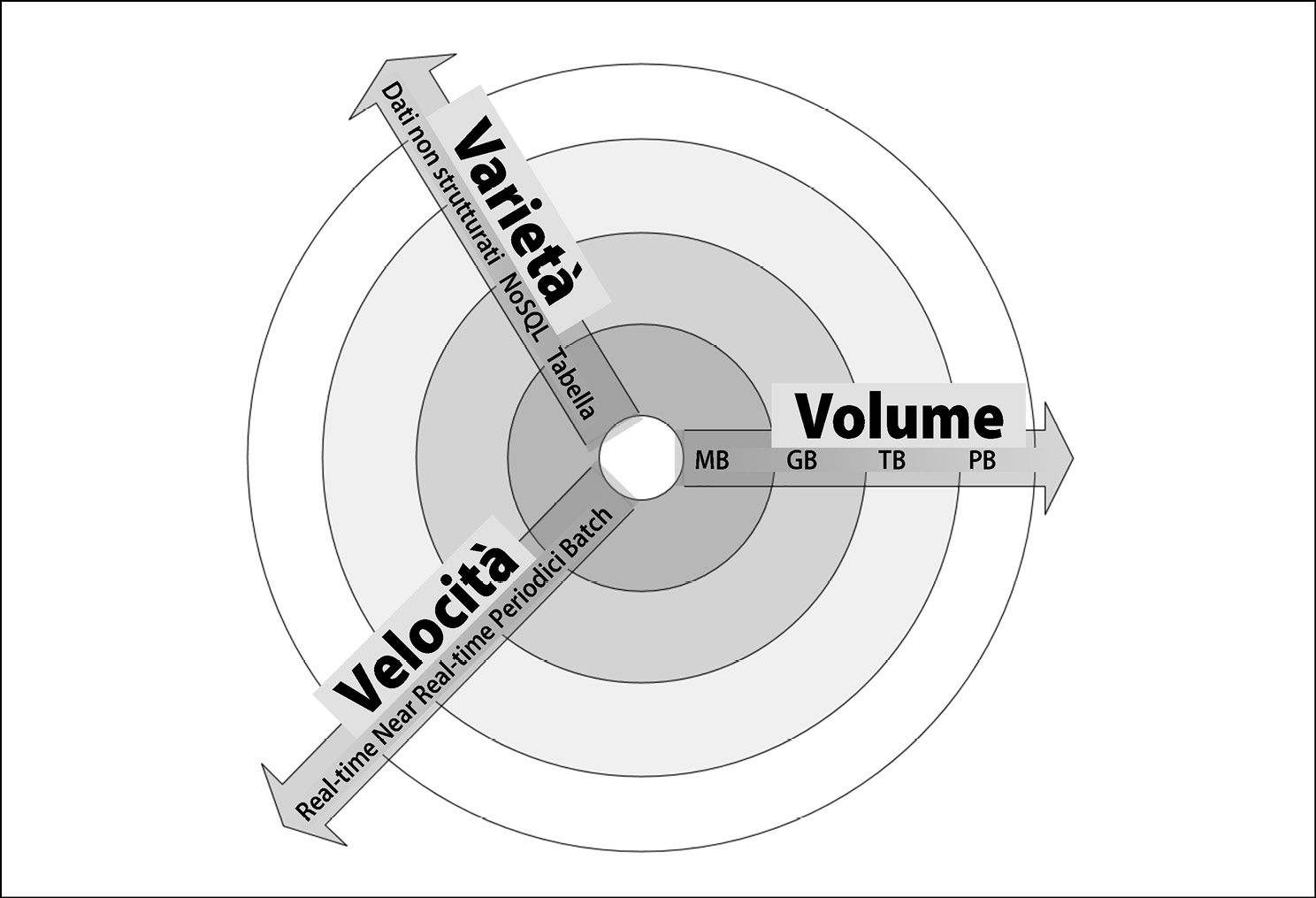
La figura sottostante mostra più in dettaglio le tre V dei dati. Al centro di questo grafico si trovano i dati più semplici possibili: piccolo volume, scarsa varietà e bassa velocità. Man mano che ci allontaniamo dal centro, la complessità dei dati aumenta, e può farlo in una o più delle tre dimensioni. Per esempio, nella dimensione della velocità, abbiamo il semplice processo Batch, seguito dal processo Periodico e quindi dal processo Near Real-Time; infine abbiamo il processo Real-Time, che è il più complesso da gestire nel reame della velocità dei dati. Per esempio, la raccolta dei feed video live prodotti da un gruppo di telecamere di monitoraggio avrà un grande volume, un’elevata velocità e una notevole varietà e per poter archiviare ed elaborare i dati in modo efficace sarà necessario realizzare un progetto appropriato. D’altra parte, un semplice file .csv prodotto da Excel avrà un volume limitato, una scarsa velocità e una limitata varietà.

Je tre V dei dati.

La dimensione del calcolo

La dimensione del calcolo riguarda le esigenze di elaborazione e calcolo del problema in questione. I requisiti di elaborazione di un algoritmo determineranno il tipo di struttura più efficiente. Per esempio, gli algoritmi di deep learning, in generale, richiedono molta potenza di elaborazione. Questo significa che per poter impiegare algoritmi di deep learning è importante poter disporre di un’architettura parallela multinodo, ove possibile.

Un esempio pratico

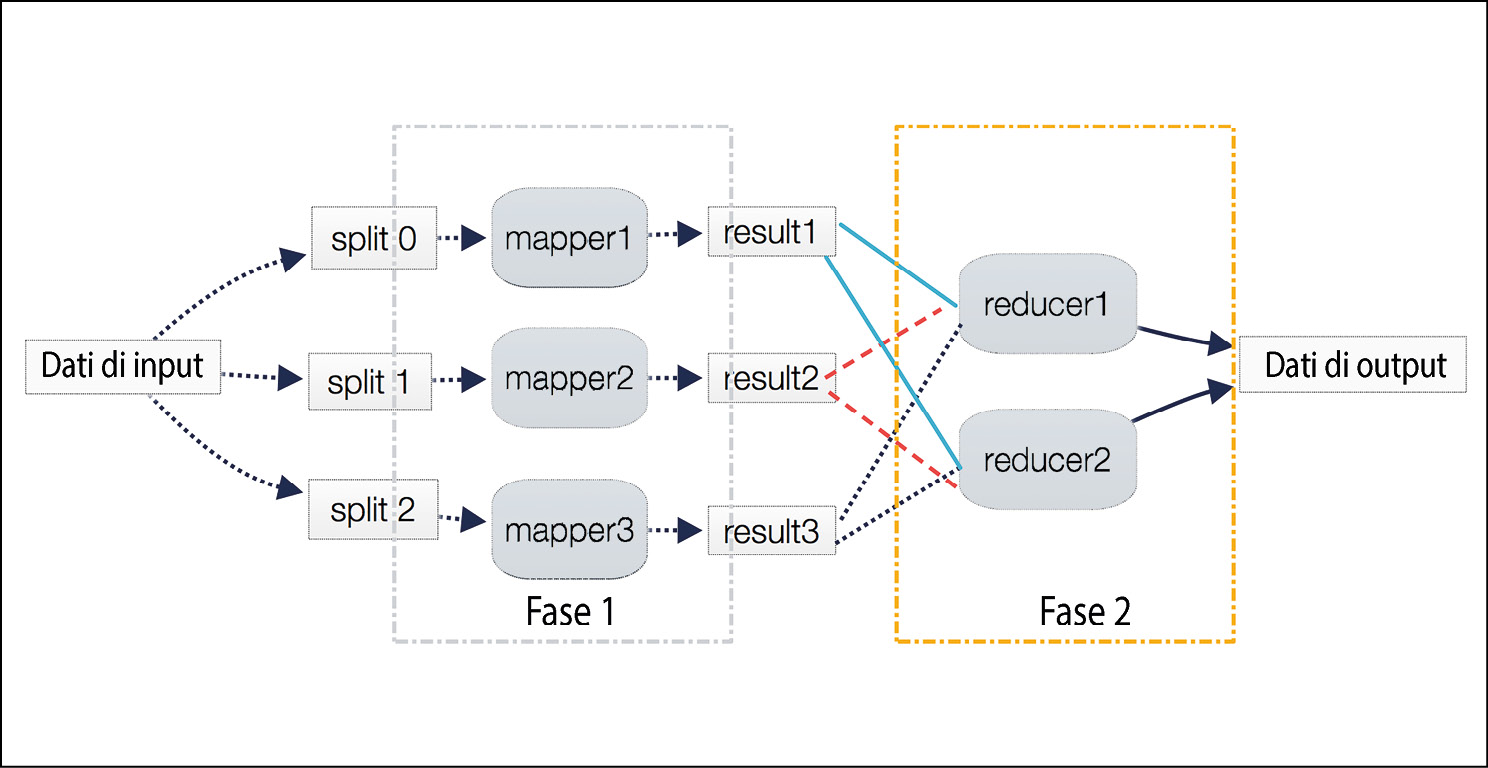
Supponiamo di voler condurre un’analisi del sentiment relativa a un video. Con l’analisi del sentiment cerchiamo di contrassegnare le diverse parti di un video con le emozioni umane: tristezza, felicità, paura, gioia, frustrazione ed estasi. È un lavoro a elevata intensità di calcolo, per il quale è necessaria molta potenza di calcolo. Come si vede nella figura qui sotto, per progettare la dimensione del calcolo, abbiamo suddiviso l’elaborazione in cinque attività, composte da due fasi. Tutta la trasformazione e la preparazione dei dati è implementata in tre mappatori, mapper. Per questo, dividiamo il video in tre diverse partizioni, chiamate split. Dopo l’elaborazione da parte dei mapper, il video risultante viene immesso nei due aggregatori, chiamati reducer. Per condurre l’analisi del sentiment, i riduttori devono raggruppare il video in base alle emozioni. Infine, i risultati vengono combinati nell’output.

Per progettare la dimensione del calcolo, abbiamo suddiviso l’elaborazione in cinque attività.

Analisi delle prestazioni

L’analisi delle prestazioni di un algoritmo è un aspetto importante della sua progettazione. Uno dei modi per stimare le prestazioni di un algoritmo è analizzarne la complessità.

La teoria della complessità studia il peso degli algoritmi. Per essere davvero utile, un buon algoritmo deve avere tre caratteristiche chiave.

• Deve essere corretto: un algoritmo non sarà molto utile se non dà le risposte giuste.
• Deve essere comprensibile: il miglior algoritmo del mondo non servirà a niente se è troppo complicato per poter essere implementato su un computer.
• Deve essere efficiente: un algoritmo che produca un risultato corretto e che sia implementabile non vi aiuterà molto se impiega mille anni o se richiede 1 miliardo di terabyte di memoria per fornire il suo risultato.

Esistono due possibili tipi di analisi per quantificare la complessità di un algoritmo.

• Analisi della complessità in termini di spazio: stima i requisiti di memoria a runtime necessari per eseguire l’algoritmo.
• Analisi della complessità in termini di tempo: stima il tempo necessario per l’esecuzione dell’algoritmo.

Analisi della complessità in termini di spazio

Stima la quantità di memoria richiesta dall’algoritmo per elaborare i dati di input. Durante l’elaborazione dei dati di input, l’algoritmo deve memorizzare alcune strutture di dati temporanee. Il modo in cui l’algoritmo è progettato influenza il numero, il tipo e la dimensione di queste strutture di dati. In questa era di calcolo distribuito e con quantità sempre più grandi di dati da elaborare, l’analisi della complessità in termini di spazio sta diventando sempre più importante. La dimensione, il tipo e il numero di queste strutture di dati determinano i requisiti di memoria per l’hardware sottostante. Le moderne strutture di dati in memoria utilizzate nel calcolo distribuito, come i Resilient Distributed Dataset (RDD), devono disporre di meccanismi efficienti di allocazione delle risorse, che siano consapevoli dei requisiti di memoria nelle diverse fasi di esecuzione dell’algoritmo.

L’analisi della complessità in termini di spazio è un must per la progettazione efficiente di algoritmi. Se non viene condotta un’analisi adeguata nella progettazione di un determinato algoritmo, una disponibilità di memoria insufficiente per le strutture di dati temporanee di cui ha bisogno può innescare inutili trasferimenti dei dati su disco, che potrebbero potenzialmente influire notevolmente sulle prestazioni e sull’efficienza dell’algoritmo stesso.

Analisi della complessità in termini di tempo

Stima quanto tempo impiegherà un algoritmo per completare il lavoro assegnato, in base alla sua struttura. A differenza della complessità in termini di spazio, la complessità in termini di tempo non dipende dall’hardware su cui verrà eseguito l’algoritmo, ma esclusivamente dalla struttura dell’algoritmo stesso. L’obiettivo generale dell’analisi della complessità in termini di tempo è quello di cercare di rispondere alle seguenti, importanti domande. Questo algoritmo sarà scalabile? In quale modo questo algoritmo gestirà dataset più grandi?

Per rispondere a queste domande, dobbiamo determinare l’effetto sulle prestazioni di un algoritmo a mano a mano che aumenta la dimensione dei dati, e assicurarci che l’algoritmo sia progettato in modo tale da renderlo non solo accurato, ma anche scalabile. Le prestazioni di un algoritmo stanno diventando sempre più importanti per dataset più grandi, nel mondo odierno dei “big data”.

In molti casi, potremmo avere a disposizione più di un approccio per progettare l’algoritmo. L’obiettivo di condurre un’analisi della complessità in termini di tempo, in questo caso, sarà il seguente.

Dato un determinato problema e più algoritmi per risolverlo, qual è il più efficiente in termini di efficienza temporale?

Ci possono essere due approcci di base per calcolare la complessità in termini di tempo di un algoritmo.

• Approccio di profilazione post-implementazione: vengono implementati più algoritmi candidati e ne vengono confrontate le prestazioni.
• Approccio teorico pre-implementazione: le prestazioni di ciascun algoritmo vengono approssimate matematicamente, prima ancora di eseguire l’algoritmo.

Il vantaggio dell’approccio teorico è che dipende solo dalla struttura dell’algoritmo, non dall’hardware effettivo che verrà utilizzato per eseguirlo, dalla scelta dello stack software impiegato a runtime o dal linguaggio di programmazione utilizzato per implementare l’algoritmo.

Stima delle prestazioni

Le prestazioni di un tipico algoritmo dipenderanno dal tipo di dati che gli vengono forniti come input. Per esempio, se i dati fossero già ordinati in base al contesto del problema che stiamo cercando di risolvere, l’algoritmo potrebbe funzionare in modo incredibilmente veloce. Se per eseguire il benchmark di questo particolare algoritmo venisse impiegato un input ordinato, otterremmo prestazioni irrealisticamente buone, che non rifletteranno le sue prestazioni reali, nella maggior parte degli scenari tipici. Per gestire questa dipendenza degli algoritmi dai dati di input, dobbiamo considerare diversi tipi di casi quando ci troviamo a eseguire un’analisi delle prestazioni.

Il caso migliore

Nel migliore dei casi, i dati forniti come input sono già organizzati in modo tale che l’algoritmo offra le sue prestazioni migliori. L’analisi del caso migliore fornisce il limite superiore delle sue prestazioni.

Il caso peggiore

Il secondo modo per stimare le prestazioni di un algoritmo è quello di cercare di trovare il tempo massimo possibile necessario perché porti a termine il lavoro in un determinato insieme di condizioni. Questa analisi del caso peggiore di un algoritmo è piuttosto utile, in quanto ci permette di garantire che, indipendentemente dalle condizioni, le prestazioni dell’algoritmo saranno sempre migliori di quanto emerge da questa analisi. L’analisi del caso peggiore è particolarmente utile per stimare le prestazioni quando si affrontano problemi complessi con grandi dataset. L’analisi del caso peggiore fornisce il limite inferiore delle prestazioni dell’algoritmo.

Il caso medio

Si inizia dividendo i vari possibili input in vari gruppi. Quindi, si conduce l’analisi delle prestazioni con uno degli input rappresentativi di ciascun gruppo. Infine, si calcola la media delle prestazioni di ciascuno dei gruppi.

L’analisi del caso medio non è sempre accurata, in quanto deve considerare tutte le diverse combinazioni e possibilità di input all’algoritmo, cosa non sempre facile.

Scelta di un algoritmo

Come facciamo a sapere qual è una soluzione migliore? Come facciamo a sapere quale algoritmo viene eseguito più velocemente? La complessità in termini di tempo e la notazione Big O sono davvero ottimi strumenti per rispondere a questo tipo di domande.

Per vederne l’utilità, prendiamo un semplice esempio in cui l’obiettivo è quello di ordinare una lista di numeri. Ci sono un paio di algoritmi in grado di svolgere il lavoro. Il problema è come scegliere quello giusto.

Innanzitutto, un’osservazione che possiamo fare è che se i numeri nella lista sono pochi, in realtà non importa quale algoritmo scegliamo per ordinarla. Quindi, se la lista è di soli 10 numeri (n = 10), non importa quale algoritmo scegliamo, poiché anche un algoritmo progettato molto male probabilmente impiegherebbe non più di qualche microsecondo. Ma non appena la dimensione della lista diventa un milione, la scelta dell’algoritmo giusto farà la differenza. Un algoritmo scritto molto male potrebbe richiedere anche un paio d’ore, mentre un algoritmo ben progettato potrebbe terminare di ordinare la lista in un paio di secondi. Quindi, per dataset di input più grandi, ha molto senso investire tempo e fatica, eseguire un’analisi delle prestazioni e scegliere un algoritmo progettato correttamente, che svolgerà il lavoro richiesto in modo efficiente.

Notazione Big O

La notazione Big O viene utilizzata per quantificare le prestazioni di vari algoritmi all’aumentare della dimensione dell’input ed è una delle metodologie più utilizzate per condurre l’analisi del caso peggiore. I seguenti paragrafi trattano i diversi tipi di notazione Big O.

Complessità costante, O(1)

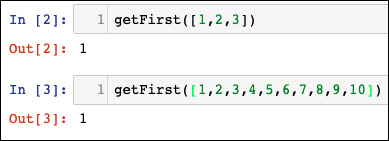
Se un algoritmo impiega la stessa quantità di tempo per essere eseguito, indipendentemente dalla dimensione dei dati di input, si dice che viene eseguito in tempo costante, rappresentato da O(1). Prendiamo l’esempio dell’accesso all’ennesimo elemento di un array. Indipendentemente dalle dimensioni dell’array, ci vorrà un tempo costante per ottenere il risultato. Per esempio, la seguente funzione restituisce il primo elemento dell’array e ha una complessità pari a O(1):

def getFirst(myList):
        return myList[0]

Ecco l’output prodotto.

• Aggiunta di un nuovo elemento in uno stack utilizzando push o rimozione di un elemento da uno stack utilizzando pop. Indipendentemente dalle dimensioni dello stack, ci vorrà lo stesso tempo per aggiungere o rimuovere un elemento.
• Accesso a un elemento di una tabella hash.
• Bucket sort.

Complessità lineare, O(n)

Si dice che un algoritmo ha una complessità lineare, rappresentata da O(n), quando il tempo di esecuzione è direttamente proporzionale alla dimensione dell’input. Un semplice esempio consiste nell’aggiungere elementi a una struttura di dati unidimensionale:

def getSum(myList):
 sum = 0
        for item in myList:
 sum = sum + item
        return sum

Notiamo il ciclo principale dell’algoritmo. Il numero di iterazioni del ciclo aumenta linearmente al crescere di n, producendo una complessità O(n):

Alcuni altri esempi di operazioni di questo tipo sono i seguenti:

• ricerca di un elemento;
• ricerca del valore minimo fra tutti gli elementi di un array.

Complessità quadratica, O(n2)

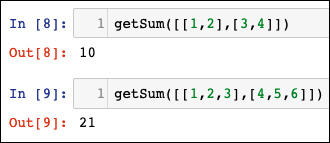
Si dice che un algoritmo viene eseguito in un tempo quadratico se il tempo di esecuzione di un algoritmo è proporzionale al quadrato della dimensione dell’input; un esempio è una semplice funzione che somma gli elementi di un array bidimensionale, come la seguente:

def getSum(myList):
        sum = 0
        for row in myList:
            for item in row:
                sum += item
        return sum

Notiamo il ciclo interno, annidato nel ciclo principale. Questo ciclo annidato conferisce al codice precedente la complessità O(n2):

Un altro esempio è l’algoritmo bubble sort.

Complessità logaritmica, O(logn)

Si dice che un algoritmo viene eseguito in un tempo logaritmico quando il tempo di esecuzione dell’algoritmo è proporzionale al logaritmo della dimensione dell’input. A ogni iterazione, la dimensione dell’input diminuisce di un fattore multiplo costante. Un esempio di complessità logaritmica è la ricerca binaria. L’algoritmo di ricerca binaria trova un determinato elemento in una struttura di dati unidimensionale, come una lista Python. Gli elementi all’interno della struttura di dati devono essere ordinati in ordine decrescente. L’algoritmo di ricerca binaria è implementato tramite una funzione denominata searchBinary, come segue:

def searchBinary(myList, item):
 first = 0
 last = len(myList) – 1
 foundFlag = False
 while(first<= last and not foundFlag):
 mid = (first + last) // 2
 if myList[mid] == item :
 foundFlag = True
 else:
 if item < myList[mid]:
 last = mid – 1
 else:
 first = mid + 1
 return foundFlag

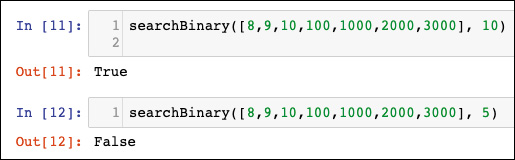
Il ciclo principale sfrutta il fatto che la lista è ordinata. Divide la lista a metà a ogni iterazione, fino ad arrivare al risultato:

Dopo aver definito la funzione, il controllo da cui dipende la ricerca di un determinato elemento si trova nelle righe 11 e 12.

Notiamo che fra i quattro tipi di notazione Big O presentati, O(n2) offre le prestazioni peggiori e O(logn) offre le prestazioni migliori. In effetti, le prestazioni O(logn) possono essere considerate il gold standard per le prestazioni di qualsiasi algoritmo (cosa che però non sempre viene raggiunta). D’altra parte, O(n2) non è così male come O(n3), ma gli algoritmi che rientrano in questa classe non possono essere utilizzati sui big data, poiché la loro complessità in termini di tempo impone dei limiti alla quantità di dati che possono elaborare, realisticamente.

Un modo per ridurre la complessità di un algoritmo consiste nello scendere a compromessi sulla sua accuratezza, producendo un tipo di algoritmo chiamato algoritmo approssimato.

L’intero processo di valutazione delle prestazioni degli algoritmi è di natura iterativa, come mostrato in questa figura.

L’intero processo di valutazione delle prestazioni degli algoritmi è di natura iterativa.

Convalida di un algoritmo

La convalida di un algoritmo conferma che sta effettivamente fornendo una soluzione matematica al problema che stiamo cercando di risolvere. Un processo di convalida dovrebbe controllare i risultati per quanti più valori di input possibili e anche per quanti più tipi di valori di input possibili.

Algoritmi esatti, approssimativi e randomizzati

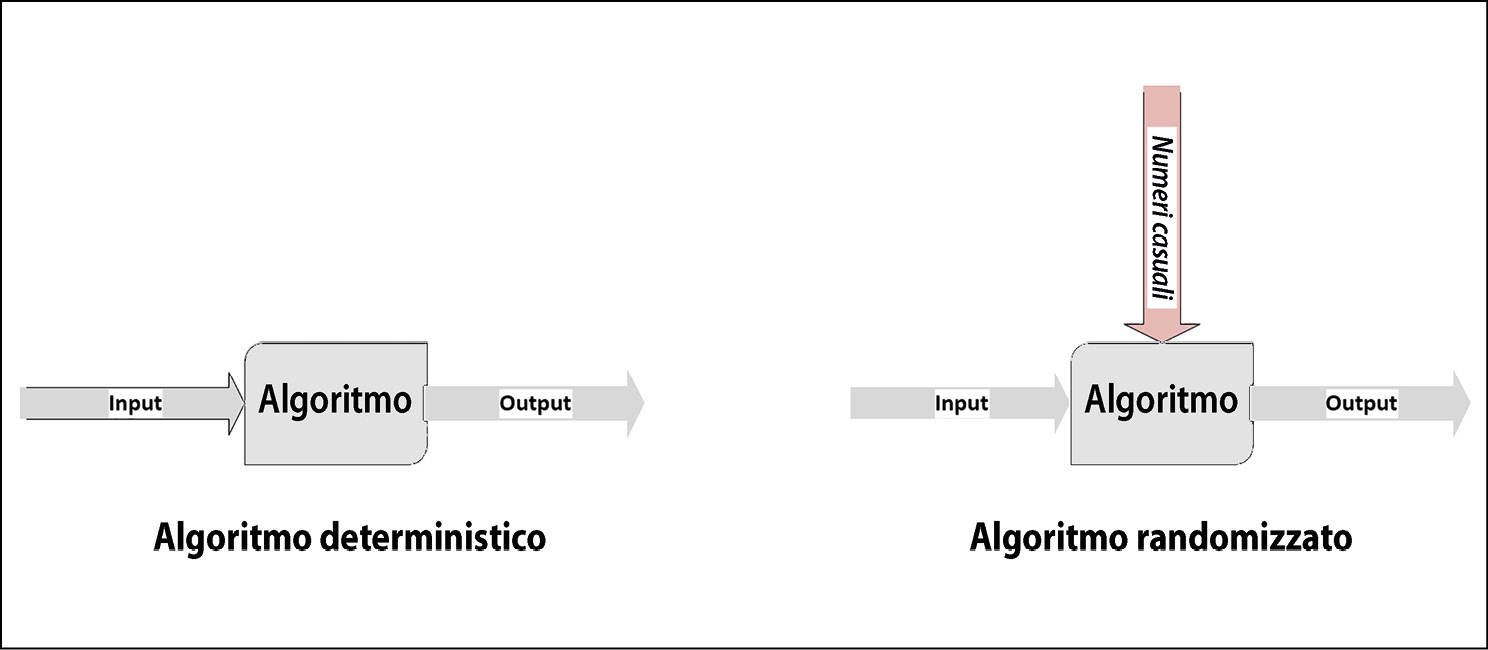
La convalida di un algoritmo dipende anche dal tipo di algoritmo, in quanto le tecniche di test sono differenti. Differenziamo prima di tutto gli algoritmi deterministici da quelli randomizzati.

Per gli algoritmi deterministici, un determinato input genera sempre esattamente lo stesso output. Ma per alcune classi di algoritmi, come input può essere presa una sequenza di numeri casuali, il che rende l’output differente a ogni esecuzione dell’algoritmo. L’algoritmo di clustering k-means (nella figura che segue) è un esempio di questo tipo.

L’algoritmo di clustering k-means.

Gli algoritmi possono anche essere suddivisi nei seguenti due tipi, sulla base delle ipotesi o delle approssimazioni utilizzate per semplificare la logica con lo scopo di renderli più veloci.

• Algoritmi esatti: ci si aspetta che gli algoritmi esatti producano una soluzione precisa senza richiedere alcuna ipotesi o approssimazione.
• Algoritmi approssimati: quando la complessità del problema è eccessiva per le risorse disponibili, semplifichiamo il problema sulla base di alcune ipotesi. Gli algoritmi approssimati, basati su queste semplificazioni o ipotesi, non ci offrono una soluzione precisa.

Facciamo un esempio per capire la differenza fra un algoritmo esatto e uno approssimato: il famoso problema del commesso viaggiatore, presentato nel 1930. Un commesso viaggiatore vi sfida a trovare il percorso più breve per un determinato venditore che deve visitare tutte le città di un elenco e poi tornare alla base. Il primo tentativo di fornire la soluzione prevedrà la generazione di tutte le possibili permutazioni delle città e la scelta della combinazione di città più economica. La complessità di questo approccio nel fornire la soluzione è O(n!), dove n è il numero di città. È ovvio che la complessità in termini di tempo inizia a diventare ingestibile oltre le 30 città.

Se il numero di città è superiore a 30, un modo per ridurre la complessità consiste nell’introdurre alcune approssimazioni e ipotesi.

Per gli algoritmi approssimati, è importante impostare le aspettative di accuratezza nella raccolta dei requisiti. La convalida di un algoritmo approssimato richiede la verifica che l’errore dei risultati rientri in un intervallo accettabile.

Spiegabilità

Quando gli algoritmi vengono utilizzati per situazioni critiche, diventa importante avere la capacità di spiegare il motivo che è alla base di ogni risultato ogni volta che sia necessario. Ciò permette di assicurarci che le decisioni basate sui risultati degli algoritmi non introducano distorsioni.

La capacità di identificare esattamente le caratteristiche che vengono utilizzate, direttamente o indirettamente, per prendere una decisione è chiamata spiegabilità di un algoritmo. Gli algoritmi, quando vengono applicati a casi d’uso critici, devono essere valutati in termini di bias e pregiudizi. L’analisi etica degli algoritmi è diventata un elemento standard del processo di convalida cui occorre sottoporre quegli algoritmi che possono influenzare processi decisionali che riguardano la vita delle persone.

Per gli algoritmi che si occupano di deep learning, la spiegabilità può essere difficile da raggiungere. Per esempio, se un algoritmo rifiuta la richiesta di un mutuo da parte di una persona, è importante pretendere trasparenza e avere la capacità di spiegarne il motivo.

La spiegabilità degli algoritmi è un’area attiva di ricerca. Una delle tecniche più efficaci, sviluppata recentemente, si chiama Local Interpretable Model-agnostic Explanation (LIME), proposta negli atti della ventiduesima conferenza internazionale Special Interest Group on Knowledge Discovery (SIGKDD) della Association for Computing Machinery (ACM) sulle scoperte della conoscenza e il data mining, nel 2016. La tecnica LIME si basa su un concetto: vengono indotti piccoli cambiamenti all’input per ogni istanza e quindi viene fatto il tentativo di mappare il confine decisionale locale per quell’istanza. In tal modo è in grado di quantificare l’influenza di ciascuna variabile di tale istanza.

Questo articolo richiama contenuti da 40 algoritmi che ogni programmatore deve conoscere.

Immagine di apertura di Michael Dziedzic su Unsplash.