Perché ricorrere alla ricerca binaria
Supponiamo di cercare una persona nell’elenco telefonico (oddio, che frase antiquata!). Il suo cognome inizia per K. Potremmo iniziare dall’inizio e continuare a sfogliare le pagine fino ad arrivare alle K. Ma è più probabile che inizieremo da una pagina centrale, perché sappiamo che la K è più a metà dell’alfabeto. Questo è l’inizio del viaggio che porta all’uso della ricerca binaria.
Oppure supponiamo di cercare una parola in un dizionario e che inizi con O. Di nuovo, inizieremo in prossimità del centro.
Supponiamo ora di accedere a Facebook. Facebook deve verificare che noi abbiamo un account, quindi, deve cercare il nostro nome-utente nel suo database. Supponiamo che il nostro nome-utente sia karlmageddon. Facebook potrebbe iniziare dalla A e cercare il nostro nome, ma ha più senso che inizi da qualche parte nel mezzo.
Questo è un problema di ricerca. E tutti questi casi usano lo stesso algoritmo per risolvere il problema: quello di ricerca binaria.
La ricerca binaria è un algoritmo; il suo input è una lista ordinata di elementi. Se l’elemento che stiamo cercando è in quella lista, la ricerca binaria restituisce la sua posizione. In caso contrario, la ricerca binaria restituisce null.
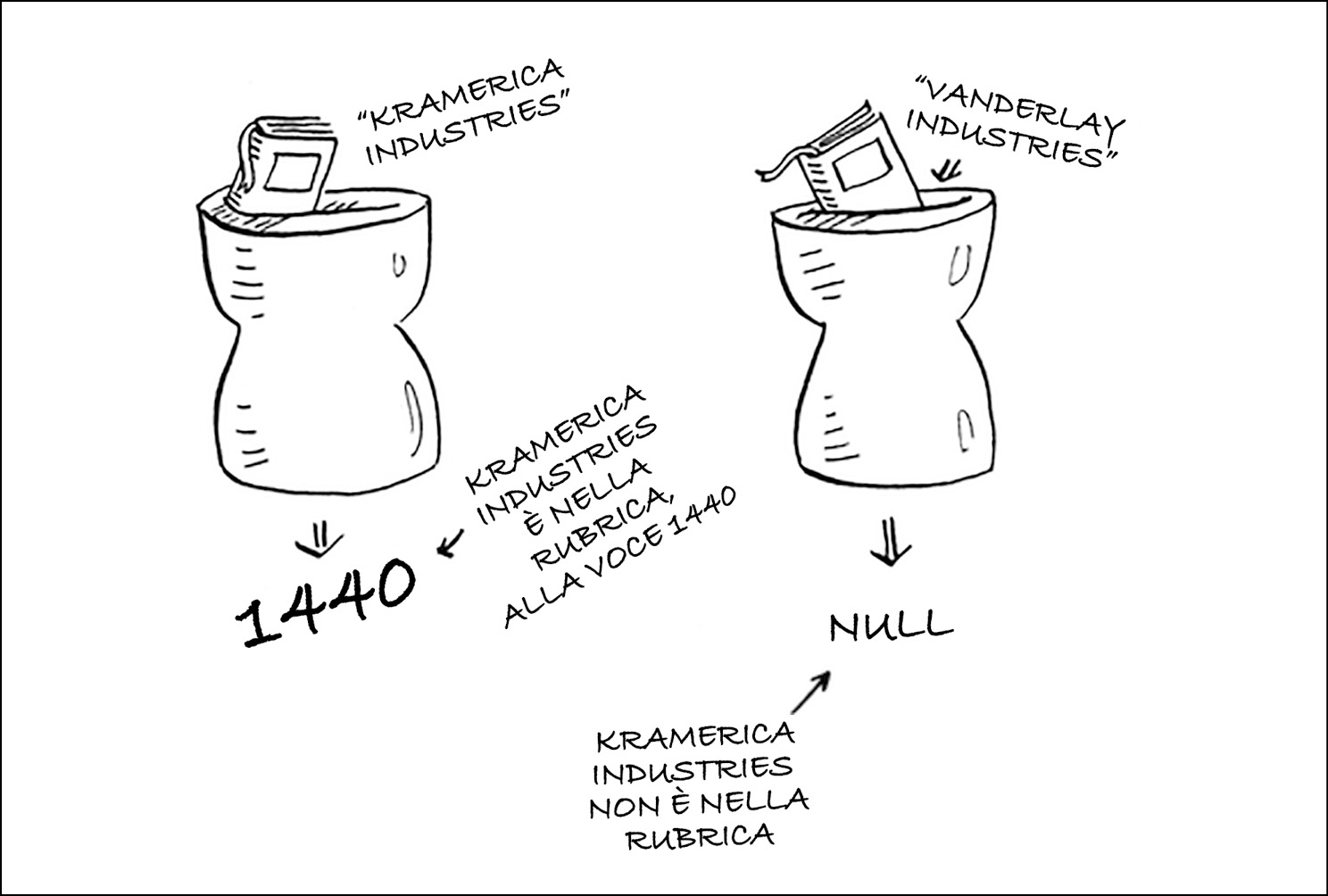
Per esempio, osserviamo la figura seguente.
Ricerca di aziende in una rubrica telefonica con la ricerca binaria.
Ecco un esempio di come funziona la ricerca binaria. Sto pensando a un numero compreso tra 1 e 100.
Bisogna indovinare il mio numero nel minor numero possibile di tentativi. Io dirò se la ciascuna ipotesi è troppo bassa, troppo alta o corretta.
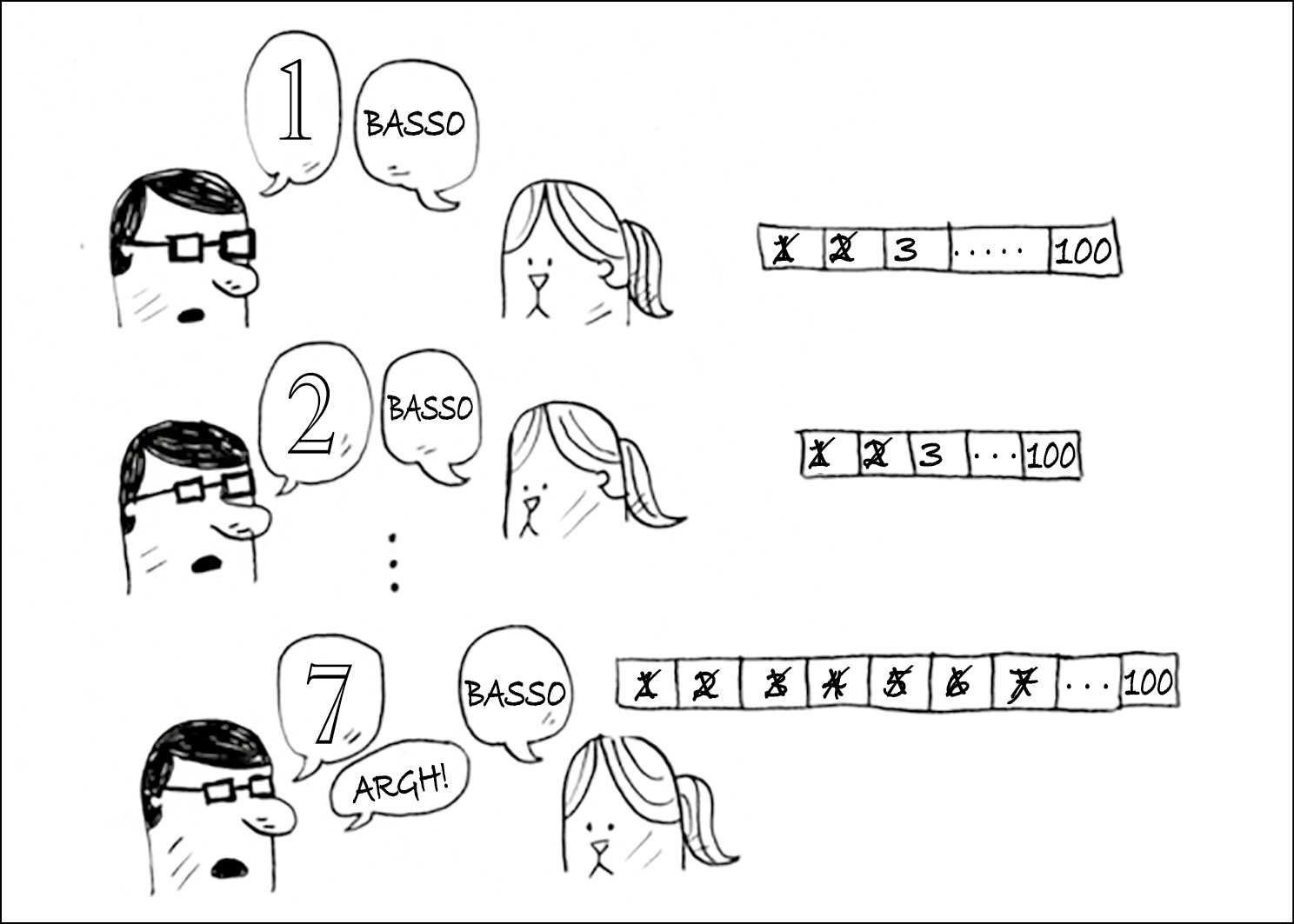
Supponiamo di iniziare a indovinare in questo modo: 1, 2, 3, 4, …. Ecco come andrebbe.
Un cattivo approccio per indovinare i numeri.
Questa è una ricerca semplice (ma forse sarebbe meglio chiamarla ricerca stupida). A ogni ipotesi, stiamo eliminando un solo numero. Se il mio numero fosse 99, ci vorrebbero 99 tentativi per arrivarci!
Un modo migliore per cercare
Ecco una tecnica migliore. Partiamo da 50.
Troppo basso, ma abbiamo appena eliminato metà dei numeri! Ora sappiamo che i numeri da 1 a 50 sono tutti troppo bassi. Prossima ipotesi: 75.
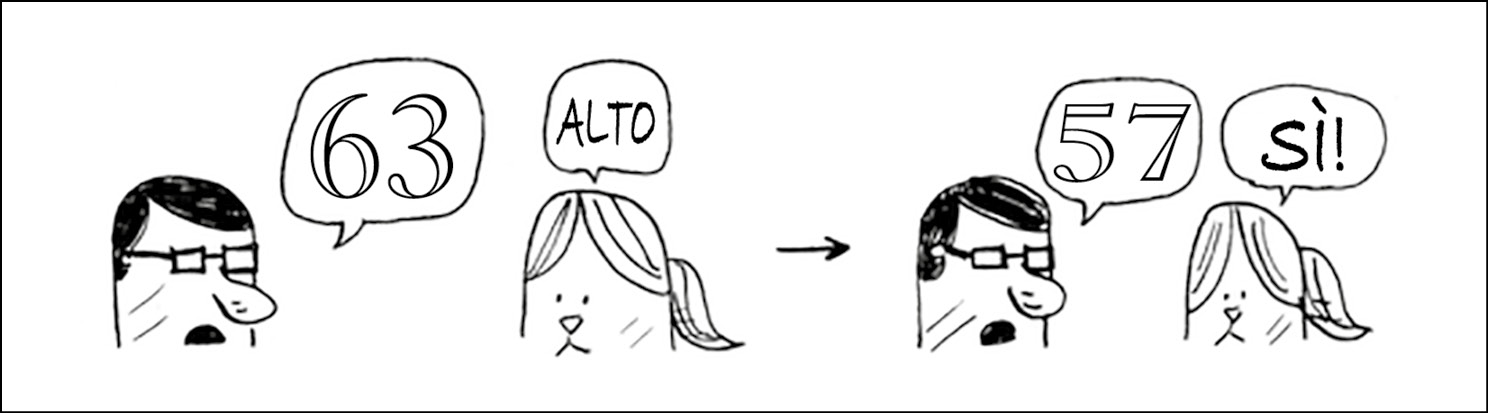
Troppo alto, ma di nuovo abbiamo ridotto la metà dei numeri rimanenti! Con la ricerca binaria, proponiamo il numero centrale ed eliminiamo ogni volta la metà dei numeri rimanenti. Il prossimo numero è 63 (a metà tra 50 e 75).
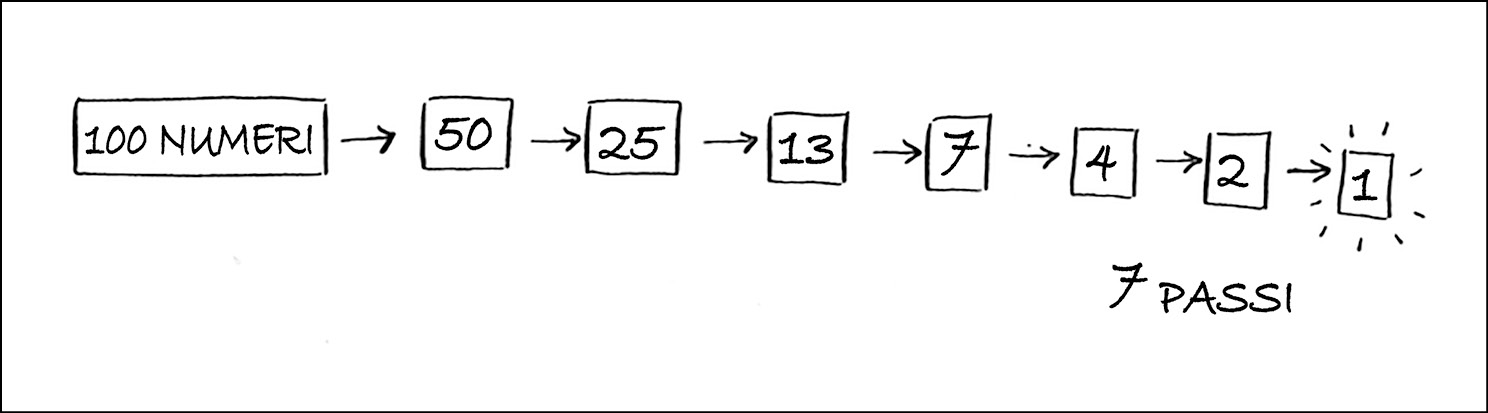
Questa è una ricerca binaria. Abbiamo appena imparato il nostro primo algoritmo! Ecco quanti numeri possiamo eliminare ogni volta.
Con la ricerca binaria eliminiamo ogni volta la metà dei numeri.
Qualsiasi sia il numero che ho in mente, dovremo fare al massimo sette ipotesi, perché a ogni ipotesi eliminiamo così tanti numeri inutili!
Leggi anche: Che cos’è un algoritmo e come progettarlo
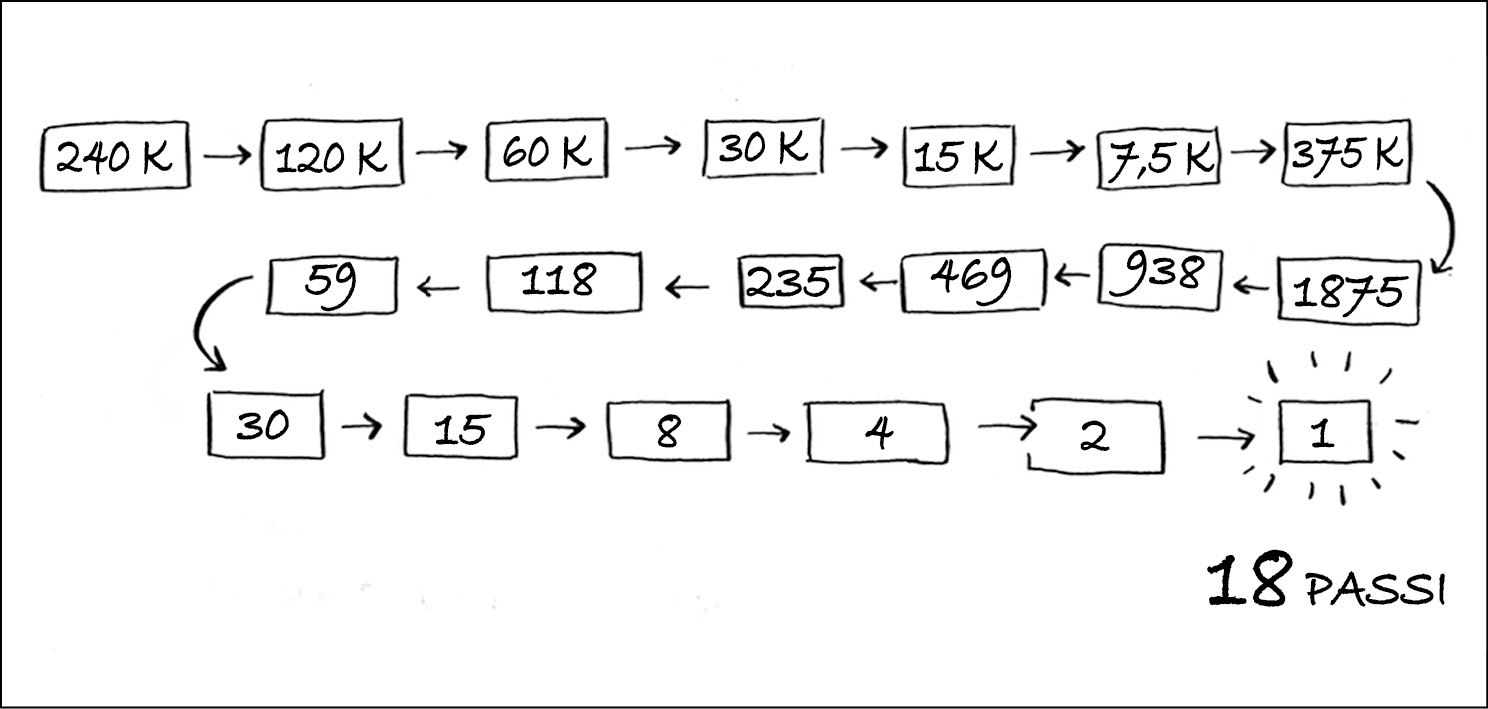
Supponiamo di stare cercando una parola nel dizionario. Il dizionario contiene 240 mila parole. Nel caso peggiore, quanti passi richiederà ogni ricerca?
La ricerca semplice potrebbe richiedere 240 mila passi, se la parola che stiamo cercando è l’ultima del dizionario. A ogni passo della ricerca binaria, invece, dimezziamo il numero di parole rimanenti, finché non ne rimane una sola.
Quindi, la ricerca binaria richiederà 18 passi: una grande differenza! In generale, per qualsiasi lista di n elementi, la ricerca binaria richiederà il log2 n passi, nel caso peggiore, mentre una ricerca semplice richiederà n passi.
Scrivere una ricerca binaria in Python
Vediamo come scrivere una ricerca binaria in Python. Il seguente esempio di codice usa gli array. Se non sappiamo come funzionano gli array, non preoccupiamoci; dobbiamo solo immaginare di memorizzare una sequenza di elementi in una fila di caselle consecutive, chiamata array. Le caselle sono numerate a partire da 0: la prima casella si trova nella posizione 0, la seconda nella posizione 1, la terza nella posizione 2 e così via.
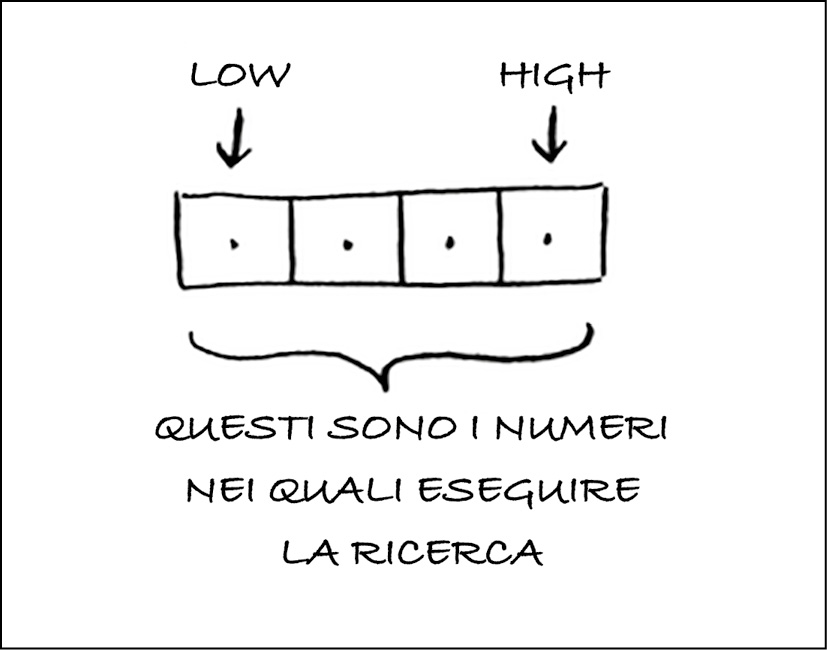
La funzione binary_search accetta un array ordinato e un elemento. Se l’elemento è contenuto nell’array, la funzione ne restituisce la posizione. Occorre registrare in quale parte dell’array dobbiamo cercare. All’inizio, si tratta dell’intero array:
low = 0
high = len(list) - 1
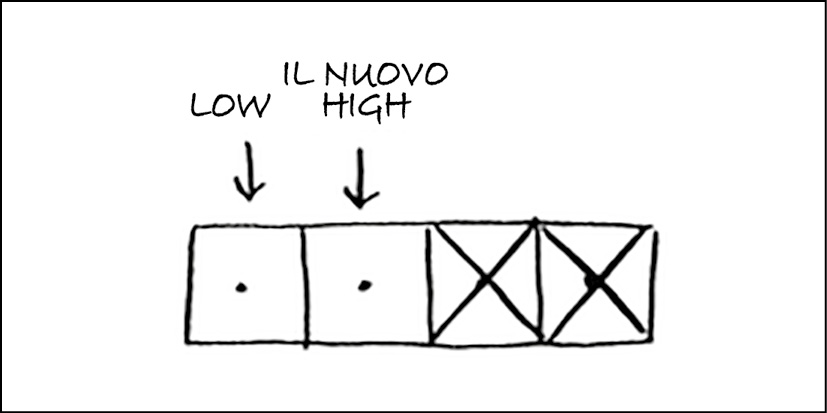
Ogni volta, controlliamo l’elemento centrale:
mid = (low + high) // 2 ➊
guess = list[mid]
➊ mid viene arrotondato automaticamente per difetto da Python se (low + high) non è un numero pari.
Se guess è troppo basso, aggiorniamo low in modo appropriato:
if guess < item:
low = mid + 1
E se guess è troppo alto, aggiorniamo high. Ecco il codice completo:
def binary_search(list, item):
low = 0 ➊
high = len(list)—1 ➊
while low <= high: ➋
mid = (low + high) // 2 ➌
guess = list[mid]
if guess == item: ➍
return mid
if guess > item: ➎
high = mid - 1
else: ➏
low = mid + 1
return None ➐
my_list = [1, 3, 5, 7, 9] ➑
print binary_search(my_list, 3) # => 1 ➒
print binary_search(my_list, -1) # => None ➓
➊ low e high tengono traccia della parte della lista in cui eseguiremo la ricerca.
➋ Finché non avremo ristretto la ricerca a un solo elemento…
➌ …controlliamo l’elemento centrale.
➍ Trovato l’elemento.
➎ guess era troppo alto.
➏ guess era troppo basso.
➐ L’elemento non è presente.
➑ Proviamolo!
➒ Ricordiamo, le liste iniziano da 0. La seconda casella ha indice 1.
➓ None significa nulla in Python. Indica che l’elemento non è stato trovato.
Tempo di esecuzione
In genere si desidera scegliere l’algoritmo più efficiente, indipendentemente dal fatto che si stia cercando di ottimizzare il tempo di esecuzione o lo spazio occupato.
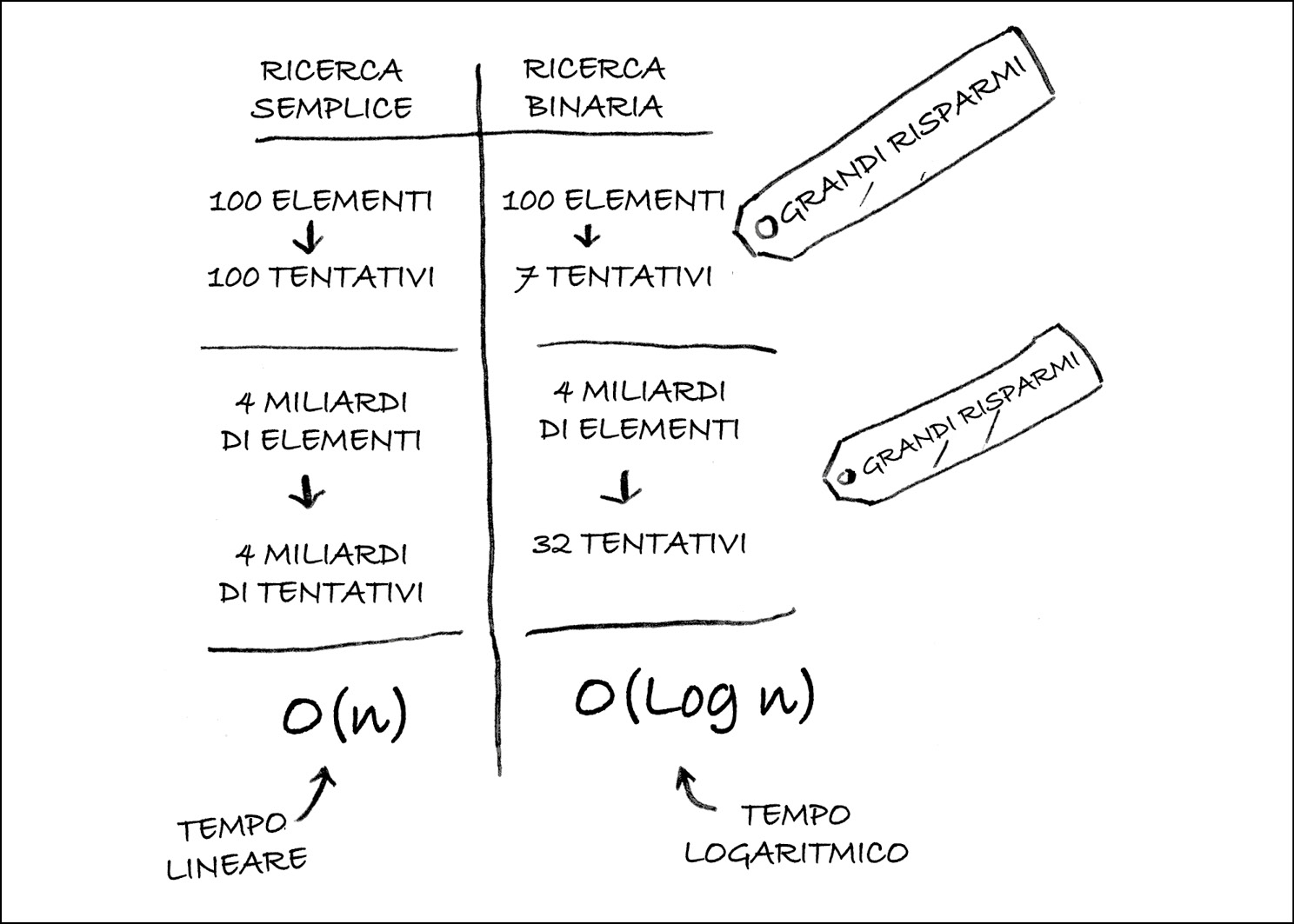
Torniamo alla ricerca binaria. Quanto tempo risparmiamo usandola? Bene, il primo approccio è stato controllare ogni numero, uno per uno. Se questa è una lista di 100 numeri, avremo bisogno di fare fino a 100 ipotesi.
Se la lista contiene 4 miliardi di numeri, dovremo fare fino a 4 miliardi di ipotesi. Quindi il numero massimo di ipotesi corrisponde alle dimensioni della lista. Questo è chiamato tempo lineare.
La ricerca binaria è diversa. Se la lista è lunga 100 elementi, avremo bisogno, al massimo, di 7 tentativi. Se la lista è lunga 4 miliardi di elementi, avremo bisogno, al massimo, di 32 tentativi. Potente, vero? La ricerca binaria viene eseguita in un tempo logaritmico (o tempo log, come dicono gli iniziati). Ecco una tabella che riassume le nostre scoperte di oggi. Buona ricerca binaria!
Tempi di esecuzione degli algoritmi di ricerca.
Questo articolo richiama contenuti da Algoritmi spiegati in modo facile.
Immagine di apertura di Markus Winkler su Unsplash.